NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables गणित अध्याय 3 दो चर वाले रैखिक समीकरण युग्म

Exercise 3.1

Question 1:
Form the pair of linear equations in the following problems, and find their solutions graphically.
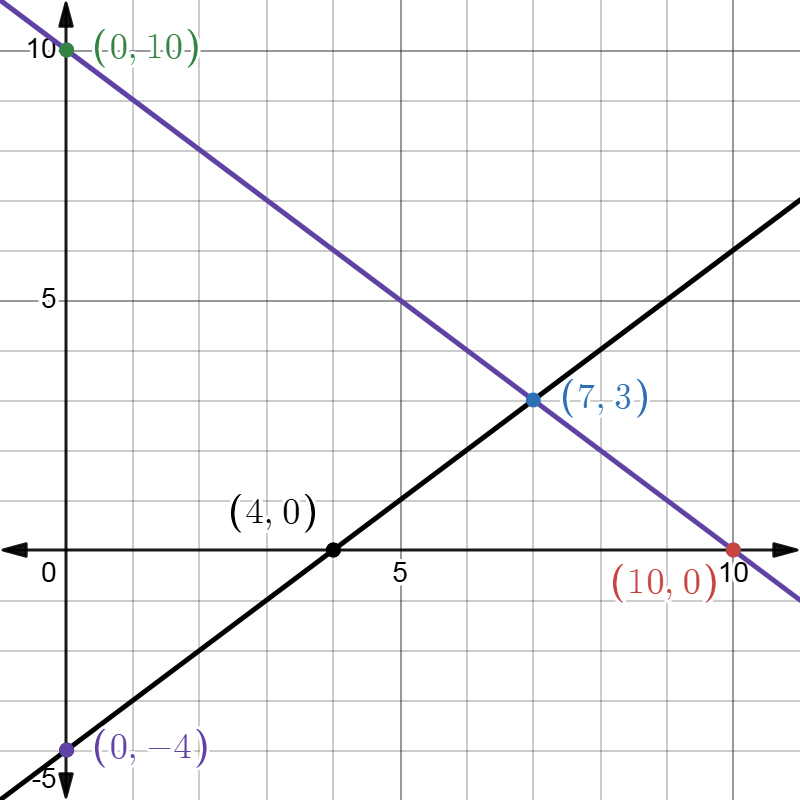
(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
कक्षा X के 10 विद्यार्थियों ने गणित प्रश्नोत्तरी में भाग लिया। यदि लड़कियों की संख्या लड़कों की संख्या से 4 अधिक है, तो प्रश्नोत्तरी में भाग लेने वाले लड़कों और लड़कियों की संख्या ज्ञात कीजिए।
Answer
Let number of girls be x and number of boys be y.
ATQ,
x +y = 10 …(1)
and, x = y + 4
\(\Rightarrow\) x – y = 4 …(2)
From equation (1), x + y = 10

x	0	10
y	10	0

From equation (2), x – y = 4

x	0	4
y	-4	0

NCERT Solutions for Class 10 Maths Chapter 3

(ii) 5 pencils and 7 pens together cost ₹ 50, whereas 7 pencils and 5 pens together cost ₹ 46. Find the cost of one pencil and that of one pen.
5 पेंसिल और 7 पेन की कीमत 50 रुपये है, जबकि 7 पेंसिल और 5 पेन की कीमत 46 रुपये है। एक पेंसिल और एक पेन की कीमत ज्ञात कीजिए।
Answer
Let the cost of one pencil be ₹ x.
and the cost of one pen be ₹ y.
ATQ,
5x + 7y = 50
and 7x + 5y = 46

Question 2:
On comparing the ratios \(\frac{a_1}{a_2}, \frac{b_1}{b_2} and \frac{c_1}{c_2}\) , find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident:
अनुपातों \(\frac{a_1}{a_2}, \frac{b_1}{b_2} और \frac{c_1}{c_2}\) की तुलना करने पर पता लगाएं कि क्या रैखिक समीकरणों के निम्नलिखित युग्मों को दर्शाने वाली रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, समान्तर हैं या संपाती हैं।
\((i) 5x – 4y + 8 = 0; 7x + 6y – 9 = 0\quad (ii) 9x + 3y + 12 = 0; 18x + 6y + 24 = 0 \\ (iii) 6x – 3y + 10 = 0; 2x – y + 9 = 0\)
Answer
(i) 5x – 4y + 8 = 0;
7x + 6y – 9 = 0
a₁ = 5, b₁ = -4, c₁ = 8
a₂ = 7, b₂ = 6, c₂ = -9
\(\frac{a_1}{a_2} = \frac{5}{7}\)
\(\frac{b_1}{b_2} = \frac{-4}{6} = \frac{-2}{3}\)
\(\frac{c_1}{c_2} = \frac{8}{-9}\)
Since, \(\frac{a_1}{a_2} ≠ \frac{b_1}{b_2}\)
So, the pairs of equations given in the question intersect at a point.

(ii) 9x + 3y + 12 = 0;
18x + 6y + 24 = 0
a₁ = 9, b₁ = 3, c₁ = 12
a₂ = 18, b₂ = 6, c₂ = 24
\(\frac{a_1}{a_2} = \frac{9}{18} =\frac{1}{2}\)
\(\frac{b_1}{b_2} = \frac{3}{6} = \frac{1}{2}\)
\(\frac{c_1}{c_2} = \frac{12}{24} = \frac{1}{2}\)
Since, \(\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}\)
So, the pairs of equations given in the question have infinite solutions and the lines are coincident.

(iii) 6x – 3y + 10 = 0;
2x – y + 9 = 0
a₁ = 6, b₁ = -3, c₁ = 10
a₂ = 2, b₂ = -1, c₂ = 9
\(\frac{a_1}{a_2} = \frac{6}{2} = 3\)
\(\frac{b_1}{b_2} = \frac{-3}{-1} = 3\)
\(\frac{c_1}{c_2} = \frac{10}{9}\)
Since, \(\frac{a_1}{a_2} = \frac{b_1}{b_2} ≠ \frac{c_1}{c_2}\)
So, the pairs of equations given in the question are parallel.

Question 3:
On comparing the ratios \(\frac{a_1}{a_2}, \frac{b_1}{b_2} and \frac{c_1}{c_2}\) , find out whether the following pair of linear equations are consistent, or inconsistent.
अनुपातों \(\frac{a_1}{a_2}, \frac{b_1}{b_2} and \frac{c_1}{c_2}\) , की तुलना करने पर पता लगाएँ कि निम्नलिखित रैखिक समीकरणों की जोड़ी सुसंगत है, या असंगत।
\((i) \;\;3x + 2y = 5 ; 2x – 3y = 7 \quad \quad(ii) 2x – 3y = 8 ; 4x – 6y = 9 \)
\((iii) \frac{3}{2} x + \frac{5}{3} y = 7; 9x – 10y = 14 \quad (iv) 5x – 3y = 11 ; – 10x + 6y = –22 \)
\((v) \frac{4}{3} x + 2y = 8; 2x + 3y = 12\)
Answer
\((i) \;\;3x + 2y = 5 ; 2x – 3y = 7 \\
\quad a_1 = 3, b_1 = 2, c_1 = 5 \\
\quad a_2 = 2, b_2 = -3, c_2 = 7\)
\(\quad\frac{a_1}{a_2} = \frac{3}{2} \\
\quad\frac{b_1}{b_2} = \frac{2}{-3} \\
\quad\frac{c_1}{c_2} = \frac{5}{7}\)
Since, \(\frac{a_1}{a_2} ≠ \frac{b_1}{b_2} \)
So, the pairs of equations given in the question are consistent.

\((ii) 2x – 3y = 8 ; 4x – 6y = 9 \\
\quad a_1 = 2, b_1 = -3, c_1 = 8 \\
\quad a_2 = 4, b_2 = -6, c_2 = 9\)
\( \quad\frac{a_1}{a_2} = \frac{2}{4} =\frac{1}{2} \\
\quad \frac{b_1}{b_2} = \frac{-3}{-6} = \frac{1}{2} \\
\quad\frac{c_1}{c_2} = \frac{8}{9}\)
Since, \(\frac{a_1}{a_2} = \frac{b_1}{b_2} ≠ \frac{c_1}{c_2} \)
So, the pairs of equations given in the question are inconsistent.

\((iii) \frac{3}{2} x + \frac{5}{3} y = 7; 9x – 10y = 14 \\
\quad a_1 = \frac{3}{2}, b_1 = \frac{5}{3}, c_1 = 7 \\
\quad a_2 = 9, b_2 = -10, c_2 = 14\)
\( \quad\frac{a_1}{a_2} = \frac{3/2}{9} =\frac{1}{6} \\
\quad \frac{b_1}{b_2} = \frac{5/3 }{-10} = \frac{-1}{6} \\
\quad\frac{c_1}{c_2} = \frac{7}{14} = \frac{1}{2}\)
Since, \(\frac{a_1}{a_2} ≠ \frac{b_1}{b_2}\)
So, the pairs of equations given in the question are consistent.

\((iv) 5x – 3y = 11 ; – 10x + 6y = –22 \\
\quad a_1 = 5, b_1 = -3, c_1 = 11 \\
\quad a_2 = -10, b_2 = 6, c_2 = -22\)
\( \quad\frac{a_1}{a_2} = \frac{5}{-10} =\frac{-1}{2} \\
\quad \frac{b_1}{b_2} = \frac{-3 }{6} = \frac{-1}{2} \\
\quad\frac{c_1}{c_2} = \frac{11}{-22} = \frac{-1}{2}\)
Since, \(\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}\)
So, the pairs of equations given in the question are consistent.

\((v) \frac{4}{3} x + 2y = 8; 2x + 3y = 12\\
\quad a_1 = \frac{4}{3}, b_1 = 2, c_1 = 8 \\
\quad a_2 = 2, b_2 =3, c_2 = 12\)
\( \quad\frac{a_1}{a_2} = \frac{4/3}{2} =\frac{2}{3} \\
\quad \frac{b_1}{b_2} = \frac{2 }{3} \\
\quad\frac{c_1}{c_2} = \frac{8}{12} = \frac{2}{3}\)
Since, \(\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}\)
So, the pairs of equations given in the question are consistent.

Question 4:
Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
निम्नलिखित में से रैखिक समीकरणों के कौन से जोड़े संगत/असंगत हैं? यदि संगत है, तो ग्राफ़िक रूप से समाधान प्राप्त करें:
(i) x + y = 5, 2x + 2y = 10
(ii) x – y = 8, 3x – 3y = 16
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
Answer
\((i) x + y = 5, 2x + 2y = 10\\
\quad a_1 = 1, b_1 = 1, c_1 = 5 \\
\quad a_2 = 2, b_2 = 2, c_2 = 10\)
\( \quad\frac{a_1}{a_2} = \frac{1}{2} \\
\quad \frac{b_1}{b_2} = \frac{1 }{2} \\
\quad\frac{c_1}{c_2} = \frac{5}{10} = \frac{1}{2}\)
Since, \(\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}\)
So, the pairs of equations given in the question are consistent.
For, x + y = 5 or x = 5 – y

NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables गणित अध्याय 3 दो चर वाले रैखिक समीकरण युग्म

For 2x + 2y = 10 or x = (10-2y)/2 = 5 – y

\((ii) x – y = 8, 3x – 3y = 16\\
\quad a_1 = 1, b_1 = -1, c_1 = 8 \\
\quad a_2 = 3, b_2 = -3, c_2 = 16\)
\( \quad\frac{a_1}{a_2} = \frac{1}{3} \\
\quad \frac{b_1}{b_2} = \frac{-1 }{-3} =\frac{1}{3} \\
\quad\frac{c_1}{c_2} = \frac{8}{16} = \frac{1}{2}\)
Since, \(\frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
So, the pairs of equations given in the question are consistent.

\((iii) 2x + y – 6 = 0, 4x – 2y -4 = 0\\
\quad a_1 = 2, b_1 = 1, c_1 = -6 \\
\quad a_2 = 4, b_2 = -2, c_2 = -4\)
\( \quad\frac{a_1}{a_2} = \frac{2}{4} = \frac{1}{2} \\
\quad \frac{b_1}{b_2} = \frac{1 }{-2} = \frac{-1}{2} \\
\quad\frac{c_1}{c_2} = \frac{-6}{-4} = \frac{3}{2}\)
Since, \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2} \)
So, the pairs of equations given in the question are consistent.
Now, for 2x + y – 6 = 0 or y = 6 – 2x

And for 4x – 2y – 4 = 0 or y = (4x-4)/2

\((iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0\\
\quad a_1 = 2, b_1 = -2, c_1 = -2 \\
\quad a_2 = 4, b_2 =-4, c_2 = -5\)
\( \quad\frac{a_1}{a_2} = \frac{2}{4} = \frac{1}{2} \\
\quad \frac{b_1}{b_2} = \frac{-2 }{-4} = \frac{1}{2} \\
\quad\frac{c_1}{c_2} = \frac{-2}{-5}\)
Since, \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2} \)
So, the pairs of equations given in the question are inconsistent.

Question 5:
Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
एक आयताकार बगीचे की आधी परिधि , जिसकी लंबाई इसकी चौड़ाई से 4 मीटर अधिक है _,36 मीटर है । बगीचे की विमाएँ ज्ञात कीजिए।
Answer
Let length and breadth of a rectanular garden be x m and y m.
ATQ,
x = y + 4 \(\Rightarrow\) x – y = 4 ..(1)
and, half Perimeter = 36 \(\Rightarrow\) \(\frac{2(l + b)}{2} = 36\)
\(\Rightarrow\) x + y = 36

Question 6:
Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
(i) intersecting lines (ii) parallel lines (iii) coincident lines
रैखिक समीकरण 2 x + 3 y – 8 = 0 दिया गया है, दो चरों में एक और रैखिक समीकरण लिखें ताकि इस प्रकार बने जोड़े का ज्यामितीय प्रतिनिधित्व हो:
(i) प्रतिच्छेद करने वाली रेखाएँ (ii) समान्तर रेखाएँ (iii) संपाती रेखाएँ
Answer
2x + 3y – 8 = 0
(i) intersecting lines
\(\Rightarrow \frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
another equation = 2x – 6y – 8 = 0
(ii) parallel lines
\(\Rightarrow \frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
another equation = 6x + 9y – 8 = 0
(iii) coincident lines
\(\Rightarrow \frac{a_1}{a_2} =\frac{b_1}{b_2} = \frac{c_1}{c_2}\)
another equation = 6x + 9y – 24 = 0

Question 7:
Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
x – y + 1 = 0 और 3 x + 2 y – 12 = 0 के ग्राफ बनाएं । इन रेखाओं और x- अक्ष द्वारा बनाए गए त्रिभुज के शीर्षों के निर्देशांक निर्धारित करें और त्रिभुजाकार क्षेत्र को छायांकित करें
Answer
x – y + 1 = 0 and 3x + 2y – 12 = 0
For, x – y + 1 = 0 or x = -1+y

For, 3x + 2y – 12 = 0 or x = (12-2y)/3

NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables गणित अध्याय 3 दो चर वाले रैखिक समीकरण युग्म

Exercise 3.2

Question 1:
Solve the following pair of linear equations by the substitution method.
प्रतिस्थापन विधि द्वारा रैखिक समीकरणों के निम्नलिखित युग्म को हल करें।
\((i)\quad x + y = 14, x – y = 4 \;\quad \quad \quad\quad(ii) s – t = 3, \frac{s}{3}+\frac{t}{2} = 6\)
\((iii) 3x – y = 3, 9x – 3y = 9 \quad\quad\quad\quad(iv) 0.2x + 0.3y = 1.3, 0.4x + 0.5y = 2.3 \)
\((v) \sqrt{2}x + \sqrt{3}y = 0, \sqrt{3}x – \sqrt{8}y = 0 (vi) \frac{3x}{2}-\frac{5y}{3}=-2, \frac{x}{3}+\frac{y}{2} = \frac{13}{6}\)
Answer
(i)\(\quad\) x + y = 14 …(1)
and, x – y = 4 …(2)
from equation (1),
\(\quad\) x = 14 – y … (3)
Putting the value of x in equation (2),
\(\quad\) (14 – y) – y = 4
\(\Rightarrow\) 14 – 2y = 4
\(\Rightarrow\)2y = 10
\(\Rightarrow\) y = 5
Putting the value of y in equation (3),
∴ x = 14 – 5
Or x = 9
Hence, x = 9 and y = 5

(ii)\(\quad\) s – t = 3 …(1)
and, \(\frac{s}{3} + \frac{t}{2}\) = 6 …(2)
From equation (1),
\(\quad\) s = 3 + t … (3)
Putting the value of s in equation (2),
\(\quad \frac{3 + t}{3} + \frac{t}{2}\) = 6
\(\Rightarrow \frac{6 + 2t + 3t}{6}\) = 6
\(\Rightarrow \) 6 + 5t = 36
\(\Rightarrow\) 5t = 30
\(\Rightarrow\) t = 6
Putting the value of t in equation (3),
∴ s = 3 + 6
Or s = 9
Hence, s = 9 and t = 6

(iii)\(\quad\) 3x – y = 3 …(1)
and, 9x – 3y = 9 …(2)
from equation (1),
\(\quad\) 3x = 3 + y … (3)
\(\quad\) x = \(\frac{3 + y}{3}\)
Putting the value of x in equation (2),
\(\quad\) 9\(\frac{3 + y}{3}\) – 3y = 9
\(\Rightarrow\) 9 + 3y – 3y = 9
\(\Rightarrow\) 9 = 9
Therefore, y has infinite values, and since x = (3+y) /3, x also has infinite values.

(iv)\(\quad\) 0.2x + 0.3y = 1.3 …(1)
and, 0.4x + 0.5y = 2.3 …(2)
from equation (1),
\(\quad\) 0.2x = 1.3 – 0.3y
\(\quad\) x = \(\frac{1.3 – 0.3y}{0.2}\)… (3)
Putting the value of x in equation (2),
\(\quad\) \(0.4(\frac{1.3 – 0.3y}{0.2})\) + 0.5y = 2.3
\(\Rightarrow\) 2(1.3 – 0.3y) + 0.5y = 2.3
\(\Rightarrow\) 2.6 – 0.6y + 0.5y = 2.3
\(\Rightarrow\) -0.1y = 2.3 – 2.6 = -0.3
\(\Rightarrow\) y = \(\frac{-0.3}{-0.1}\)
\(\Rightarrow\) y = 3
Putting the value of y in equation (3),
∴ x = \(\frac{1.3 – 0.3 \times 3}{0.2}\)
or x = \(\frac{0.4}{0.2}\)
or x = 2
Hence, x = 2 and y = 3

(v)\(\quad\) \(\sqrt{2}x + \sqrt{3}y\) = 0 …(1)
and, \(\sqrt{3}x – \sqrt{8}y\) = 0 …(2)
From equation (1),
\(\quad \sqrt{2}x + \sqrt{3}y\) = 0
\(\Rightarrow \sqrt{2}x = – \sqrt{3}y\)
\(\Rightarrow x = \frac{-\sqrt{3}}{\sqrt{2}y}\) … (3)
Putting the value of x in equation (2),
\(\quad \sqrt{3} \times \frac{-\sqrt{3}}{\sqrt{2}y} – \sqrt{8}y\) = 0
Hence, x = 0 and y = 0

\((vi) \quad\frac{3x}{2}-\frac{5y}{3}=-2…(1)\\
\quad\quad\frac{x}{3}+\frac{y}{2} = \frac{13}{6}…(2)\)
From equation (1)
\(\quad\) 9x – 10y = -12
\(\Rightarrow\) 9x = -12 + 10y
\(\Rightarrow\) x = \(\frac{-12 + 10y}{9}\)…(3)
Putting the value of x in equation (2),
\(\quad \frac{\frac{-12+10y}{9}}{3} + \frac{y}{2} = \frac{13}{6}\)
\(\Rightarrow \frac{-12 + 10y}{27} + \frac{y}{2} = \frac{13}{6}\)
\(\Rightarrow \frac{-24 + 20y + 27y}{54} = \frac{13}{6}\)
\(\Rightarrow\) -24 + 47y =\( \frac{13}{6} \times 54\)
\(\Rightarrow\) 47y = 117 + 24
\(\Rightarrow\) y = \(\frac{141}{47}\)
\(\Rightarrow\) y = 3
Putting the value of y in equation (3),
\(\Rightarrow\) x = \(\frac{-12 + 10(3)}{9}\)
\(\Rightarrow\) x = \(\frac{18}{9}\)
\(\Rightarrow\) x = 2
Hence, x = 2 and y = 3

Question 2:
Solve 2x + 3y = 11 and 2x – 4y = – 24 and hence find the value of ‘m’ for which y = mx + 3.
2x + 3y = 11 और 2x – 4y = – 24 को हल करें और इससे ‘m ‘ का मान ज्ञात करें जिसके लिए y = mx + 3 है।
Answer
2x + 3 y = 11 …(1)
and 2x – 4y = – 24…(2)
From equation (1),
\(\quad\)2x + 3y = 11
\(\Rightarrow\) x = \(\frac{11 – 3y}{2}\) …(3)
Putting the value of x in equation (2),
\(\quad 2\times \frac{11 – 3y}{2}\) – 4y = – 24
\(\Rightarrow\) 11 – 3y – 4y = – 24
\(\Rightarrow\) – 7y = – 24 – 11
\(\Rightarrow\) y = \(\frac{-35}{-7}\)
\(\Rightarrow\) y = 5
Putting the value of y in equation (3),
\(\quad\) x = \(\frac{11 – 3\times 5}{2}\)
\(\Rightarrow\) x = \(\frac{-4}{2}\)
\(\Rightarrow\) x = -2
Hence, x = – 2 and y = 5
Now, y = mx + 3
Putting x = – 2 and y = 5
\(\quad\)5 = – 2 m + 3
\(\Rightarrow\) m = – 1

Question 3:
Form the pair of linear equations for the following problems and find their solution by substitution method.
निम्नलिखित समस्याओं के लिए रैखिक समीकरणों की जोड़ी बनाएं और ज्ञात करें प्रतिस्थापन विधि द्वारा उनका हल
(i) The difference between two numbers is 26 and one number is three times the other. Find them.
(i) दो संख्याओं के बीच का अंतर 26 है और एक संख्या दूसरी की तीन गुनी है। उन्हें ज्ञात कीजिए।
Answer
Let the two numbers be x and y.
ATQ,
\(\quad\) x = 3y ……………… (1)
\(\quad\) x – y = 26 …………(2)
From equation (1),
\(\quad\) x = 3y……………(3)
Putting the value of x in equation (2),
\(\quad\) 3y – y = 26
\(\Rightarrow\) 2y = 26
\(\Rightarrow\) y = 13
Hence, the numbers are 13 and 39.

(ii) The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them.
(ii) दो संपूरक कोणों में से बड़ा कोणों से छोटे कोणों से 18 डिग्री अधिक है। उन्हें ज्ञात कीजिए।
Answer
Let the larger angle be x ^oand the smaller angle be y ^o.
We know that the sum of two supplementary pairs of angles is always 180 ^o.
ATQ,
\(\quad\) x + y = 180 ^o……………. (1)
and x – y = 18 ^o……………..(2)
From equation (1), x = 180 ^o– y …………. (3)
Putting the value of x in equation (2),
\(\quad\) 180 ^o– y – y =18 ^o
\(\Rightarrow\) -2y = 18 ^o – 180 ^o= – 162 ^o
\(\Rightarrow\) y = \(\frac{-162^0}{-2} = 81^0\)
Putting the value of y in (3),
\(\quad\) x = 180 ^o– 81 ^o= 99 ^o
Hence, the angles are 99 ^oand 81 ^o.

(iii) The coach of a cricket team buys 7 bats and 6 balls for ₹ 3800. Later, she buys 3 bats and 5 balls for ₹ 1750. Find the cost of each bat and each ball.
(iii) एक क्रिकेट टीम का कोच 3800 रुपये में 7 बल्ले और 6 गेंद खरीदता है। बाद में, वह 1750 रुपये में 3 बल्ले और 5 गेंद खरीदता है। प्रत्येक बल्ले और प्रत्येक गेंद की कीमत ज्ञात कीजिए।
Answer
Let the cost of a bat be x and the cost of a ball be y.
ATQ,
\(\quad\) 7x + 6y = 3800 ………………. (1)
\(\quad\)and, 3x + 5y = 1750 ………………. (2)
From equation (1),
\(\quad\) 7x + 6y = 3800
\(\Rightarrow\) x = \(\frac{3800-6y}{7}\)………………..(3)
Putting the value of x in equation (2),
\(\quad 3\left(\frac{3800-6y}{7}\right)\) + 5y =1750
\(\Rightarrow \frac{11400 – 18y + 35y}{7} = 1750\)
\(\Rightarrow\) 11400 + 17y = 1750 \(\times\) 7
\(\Rightarrow\) 17y = 12250 – 11400
\(\Rightarrow\) y = \(\frac{850}{17}\)
\(\Rightarrow\) y = 50
Putting the value of y in equation (3),
\(\Rightarrow\) x = \(\frac{3800-6\times 50}{7}\)
\(\Rightarrow\) x = \(\frac{3800-300}{7}\)
\(\Rightarrow\) x = \(\frac{3500}{7}\)
\(\Rightarrow\) x = 500
Hence, the cost of a bat is Rs 500, and the cost of a ball is Rs 50.

(iv) The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is ₹ 105 and for a journey of 15 km, the charge paid is ₹ 155. What are the fixed charges and the charge per km? How much does a person have to pay for travelling a distance of 25 km?
(iv) किसी शहर में टैक्सी के किराये में एक निश्चित किराया और तय की गई दूरी का किराया शामिल होता है। 10 किलोमीटर की दूरी के लिए चुकाया जाने वाला किराया 105 रुपये है और 15 किलोमीटर की यात्रा के लिए चुकाया जाने वाला किराया 155 रुपये है। तय किराया और प्रति किलोमीटर किराया क्या है? 25 किलोमीटर की दूरी तय करने के लिए एक व्यक्ति को कितना किराया देना होगा?
Answer
Let the fixed charge be Rs x and the per km charge be Rs y.
ATQ,
\(\quad\) x + 10y = 105 …………….. (1)
\(\quad\) x + 15y = 155 …………….. (2)
From equation (1),
\(\quad\) x + 10y = 105
\(\Rightarrow\) x = 105 – 10y ………………. (3)
Putting the value of x in equation (2),
\(\quad\) 105 – 10y + 15y = 155
\(\quad\) 5y = 155 – 105
\(\quad\) y = 10
Putting the value of y in equation (3),
\(\quad\) x = 105 – 10 × 10 = 5
Hence, the fixed charge is Rs 5 and the per km charge = Rs 10
Charge for 25 km = x + 25y = 5 + 250 = Rs 255

(v) A fraction becomes \(\frac{9}{11}\), if 2 is added to both the numerator and the denominator. If, 3 is added to both the numerator and the denominator it becomes \(\frac{5}{6}\). Find the fraction.
(v) एक भिन्न \(\frac{9}{11}\) हो जाती है, यदि अंश और हर दोनों में 2 जोड़ दिया जाए। यदि अंश और हर दोनों में 3 जोड़ दिया जाए तो यह \(\frac{5}{6}\) हो जाती है। भिन्न ज्ञात कीजिए।
Answer
Let the fraction be \(\frac{x}{y}\).
ATQ,
\(\quad \frac{x+2}{y+2} = \frac{9}{11}\)
\(\quad\) 11x + 22 = 9y + 18
\(\quad\) 11x – 9y = -4 …………….. (1)
\(\quad \frac{x+3}{y+3} = \frac{5}{6}\)
\(\quad\) 6x + 18 = 5y +15
\(\quad\) 6x – 5y = -3 ………………. (2)
From equation (1),
\(\quad\) 11x – 9y = – 4
\(\Rightarrow\) x = \(\frac{-4+9y}{11}\) …………….. (3)
Putting the value of x in equation (2),
\(\quad 6\times \frac{-4+9y}{11}\) -5y = -3
\(\quad \)-24 + 54y – 55y = -33
\(\quad\) -y = – 33 + 24
\(\quad\) y = 9
Putting the value of y in equation (3),
\(\quad\) x = \(\frac{-4+9×9}{11}\)
\(\quad\) x = 7
Hence, the fraction is \(\frac{7}{9}\).

(vi) Five years hence, the age of Jacob will be three times that of his son. Five years ago, Jacob’s age was seven times that of his son. What are their present ages?
(vi) पाँच वर्ष बाद, जैकब की आयु उसके पुत्र की आयु से तीन गुनी हो जाएगी। पाँच वर्ष पहले, जैकब की आयु उसके पुत्र की आयु से सात गुनी थी। उनकी वर्तमान आयु क्या है?
Answer
Let the age of Jacob and his son be x and y, respectively.
ATQ,
\(\quad\) (x + 5) = 3(y + 5)
\(\quad\) x + 5 = 3y + 15
\(\quad\) x – 3y = 10 …………………………………….. (1)
and, (x – 5) = 7(y – 5)
\(\Rightarrow\) x – 5 = 7y – 35
\(\Rightarrow\) x – 7y = -30 ………………………………………. (2)
From equation (1),
\(\quad\) x – 3y = 10
\(\quad\) x = 10 + 3y……………………. (3)
Putting the value of x in equation (2),
\(\quad\) 10 + 3y – 7y = -30
\(\Rightarrow\) -4y = -30 – 10 = – 40
\(\Rightarrow\) y = 10
Putting the value of y in equation (3),
\(\quad\) x = 3 x 10 + 10 = 40
Hence, the present age of Jacob and his son is 40 years and 10 years, respectively.

NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables गणित अध्याय 3 दो चर वाले रैखिक समीकरण युग्म

Exercise 3.3

Question 1:
Solve the following pair of linear equations by the elimination method and the substitution method :
\(\quad\) (i) x + y = 5 and 2x – 3y = 4 \(\quad\)\(\quad\) \(\quad\) \(\quad\) (ii) 3x + 4y = 10 and 2x – 2y = 2
\(\quad\) (iii) 3x – 5y – 4 = 0 and 9x = 2y + 7 \(\quad\) (iv) \(\frac{x}{2} + \frac{2y}{3} = -1\) and x – \(\frac{y}{3}\) = 3
Answer
(i) x + y = 5 ……..(1)
and 2x – 3y = 4 ……(2)
By Substitution Method,
From equation (1),
\(\quad\) x + y = 5
\(\Rightarrow\) x = 5 – y …..(3)
Putting the value of x in equation (2),
\(\quad\) 2 (5 – y) – 3y = 4
\(\Rightarrow\) 10 – 2 y – 3y = 4
\(\Rightarrow\)-5 y = 4 – 10
\(\Rightarrow\) y = \(\frac{6}{5}\)
Putting the value of y in equation (3),
\(\quad\) x = 5 – \(\frac{6}{5}\)
\(\Rightarrow\) x = \(\frac{19}{5}\)
Hence, x = \(\frac{19}{5}\) and y = \(\frac{6}{5}\)

(ii) 3x + 4y = 10 … (1)
and 2x – 2y = 2 … (2)
From equation (1),
\(\quad\) 3x + 4y = 10
\(\Rightarrow\) x = \(\frac{10 – 4y}{3}\) ….(3)
Putting the value of x in equation (2),
\(\quad\) 2 \(\frac{10 – 4y}{3}\) – 2 y = 2
\(\Rightarrow\) \(\frac{20 – 8y – 6y}{3}\) = 2
\(\Rightarrow\) 20 – 14y = 6
\(\Rightarrow\) y = 1
Putting the value of y in equation (3),
\(\quad\) x = \(\frac{10 – 4(1)}{3}\)
\(\quad\) x = 2
Hence, x = 2 and y = 1

(iii) 3x – 5y – 4 = 0 …(1)
\(\quad\)and 9x = 2y + 7 \(\Rightarrow\) 9x – 2y = 7 …(2)
From equation (1),
\(\quad\) 3x – 5y – 4 = 0
\(\Rightarrow\) x = \(\frac{5y + 4}{3}\) … (3)
Putting the value of x in equation (2),
\(\quad 9\times\left(\frac{5y + 4}{3}\right) – 2y = 7\)
\(\quad\) 15y + 12 -2y = 7
\(\quad\) 13y = – 5
\(\quad\) y = \(\frac{-5}{13}\)
Putting the value of y in equation (3),
\(\Rightarrow\) x = \(\frac{5\times\left(\frac{-5}{13}\right) + 4}{3}\)
\(\Rightarrow\) x = \(\frac{-25 + 52}{13 \times 3}\)
\(\Rightarrow\) x = \(\frac{27}{13\times3}\)
\(\Rightarrow\) x = \(\frac{9}{13}\)
Hence, x = \(\frac{9}{13}\) and y = \(\frac{-5}{13}\)

(iv) \(\frac{x}{2} + \frac{2y}{3} = -1\) … (1)
and x – \(\frac{y}{3}\) = 3 …( 2)
From equation (1),
\(\quad\) \(\frac{x}{2} + \frac{2y}{3} = -1\)
\(\Rightarrow \frac{3x + 4y}{6} = -1\)
\(\Rightarrow\) 3x + 4y = -6
\(\Rightarrow\) x = \(\frac{-6 – 4y}{3}\) … (3)
Putting the value of x in equation (2),
\(\quad \frac{-6 – 4y}{3} – \frac{y}{3}\) = 3
\(\Rightarrow \frac{-6 – 4y – y}{3} = 3\)
\(\Rightarrow\) -6 – 5y = 9
\(\Rightarrow\) – 5y = 9 + 6
\(\Rightarrow\) y = \(\frac{15}{-5}\) = -3
Putting the value of y in equation (3),
\(\Rightarrow\) x = \(\frac{-6 – 4(-3)}{3}\)
\(\Rightarrow\) x = \(\frac{-6 + 12}{3}\)
\(\Rightarrow\) x = 2
Hence, x = 2 and y = – 3

NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables गणित अध्याय 3 दो चर वाले रैखिक समीकरण युग्म

Question 2:
Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method :

(i) If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to 1. It becomes \(\frac{1}{2}\) if we only add 1 to the denominator. What is the fraction?
Answer
Let the fraction be \(\frac{x}{y} \)
ATQ,
\(\frac{x + 1}{y – 1} = 1\)
\(\Rightarrow\) x + 1 = y – 1
\(\Rightarrow\) x – y = – 2 … (1)
and \(\frac{x}{y + 1} = \frac{1}{2}\)
\(\Rightarrow\) 2x = y + 1
\(\Rightarrow\) 2x – y = 1 … (2)
Subracting (2) from (1),
\(\;\)x – y = – 2
2x – y = 1
– \ + \(\quad\) –
——————
-x \(\quad\)= -3 \(\Rightarrow\) x = 3
putting the value of x in equation (2),
\(\Rightarrow\) 2(3) – y = 1
\(\Rightarrow\) y = 5
Hence, the fraction is \(\frac{3}{5}\).

(ii) Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?
Answer
Let the present age of Nuri be x years
and the present age of Sonu be y years.
ATQ
\(\quad\) x – 5 = 3(y – 5)
\(\Rightarrow\) x – 3y = -10…………………………………..(1)
and, x + 10 = 2(y +10)
\(\Rightarrow\) x – 2y = 10…………………………………….(2)
Subtract (2) from (1)
x – 3y = -10
x – 2y = 10
– \(\quad\) + \(\quad\) –
———————–
\(\quad\) – y = -20
\(\quad\) y = 20
Putting the value of y in equation (1)
\(\quad\) x – 3.20 = -10
\(\Rightarrow\) x – 60 = -10
\(\Rightarrow\)x = 50
Therefore, Age of Nuri is 50 years Age of Sonu is 20 years

(iii) The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
Answer
Let the unit digit and tens digit of a number be x and y, respectively.
Number = 10\(\times\) tens digit + unit digit
\(\quad\) = 10y + x
On reversing the order of the digits = 10x + y
ATQ,
\(\quad\) x + y = 9 …(1)
and, 9(10y + x) = 2(10x + y)
\(\Rightarrow\) 90 + 9x = 20x + 2y
\(\Rightarrow\) -11x + 88y = 0
\(\Rightarrow\) -11(x – 8y) = 0 \(\Rightarrow\) x – 8y = 0…(2)
Subtracting (1) from (2),
x + y = 9
x – 8y = 0
– \(\quad\) + \(\quad\) –
——————-
\(\quad\) 9y = 9
\(\Rightarrow\) y = 1
Putting the value of y in equation (i),
\(\quad\) x + 1= 9
\(\Rightarrow\) x = 8
Hence, the number = 10\(\times\)1 + 8 = 18

(iv) Meena went to a bank to withdraw ₹ 2000. She asked the cashier to give her ₹ 50 and ₹ 100 notes only. Meena got 25 notes in all. Find how many notes of ₹ 50 and ₹ 100 she received.
Answer
Let the number of ₹ 50 notes be x and the number of ₹ 100 notes be y.
ATQ,
\(\quad\) x + y = 25 … (1)
and, 50x + 100y = 2000
(\Rihgtarrow\) 50 (x + 2y) = 2000
(\Rightarrow\) x + 2y = 40… (2)
Subtracting (2) from (1)
\(\quad\) x + y = 25
\(\quad\) x + 2y = 40
\(\quad\) – \(\;\) – \(\;\) –
———————-
\(\quad\) -y = -15 \(\Rightarrow\) y = 15
putting the value of y in equation (1),
\(\quad\) x + 15 = 25
\(\Rightarrow\)x = 10
Hence, Meena has 10 notes of ₹ 50 and 15 notes of ₹ 100.

(v) A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid ₹ 27 for a book kept for seven days, while Susy paid ₹ 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.
Answer
Let the fixed charge be ₹ x
and the charge for each extra day be ₹ y.
ATQ,
\(\quad\) x + 4y = 27 … (1)
and, x+ 2y = 21 … (2)
Subtracting (2) from (1),
x + 4y = 27
x + 2y = 21
– \(\quad\) – \(\quad\) –
———————
\(\quad\) 2y = 6 \(\Rightarrow\) y = 3
Putting the vaule of y in equation (1),
\(\quad\) x + 12 = 27 \(\Rightarrow\) x = 15
Hence, the fixed charge is ₹ 15.
And the charge per day is ₹ 3.

NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables गणित अध्याय 3 दो चर वाले रैखिक समीकरण युग्म

BrightWay Coaching Academy

Post Views: 53

NCERT Solutions for Class 10 Maths Chapter 3