NCERT Solutions for Class 10 Maths Chapter 2 Polynomials
Thank you for reading this post, don't forget to subscribe!Exercise 2.1
Question 1:
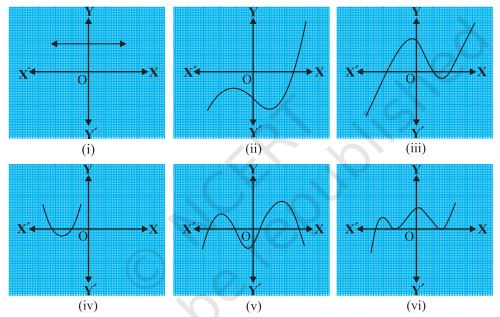
The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
Answer
(i) In the given graph, the number of zeroes of p(x) is 0.
(ii) In the given graph, the number of zeroes of p(x) is 1.
(iii) In the given graph, the number of zeroes of p(x) is 3.
(iv) In the given graph, the number of zeroes of p(x) is 2.
(v) In the given graph, the number of zeroes of p(x) is 4.
(vi) In the given graph, the number of zeroes of p(x) is 3.
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials
Exercise 2.2
Question 1:
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
\(\quad (i)\; x^2 – 2x – 8 \quad (ii)\; 4s^2 – 4s + 1 \quad (iii)\; 6x^2 – 3 – 7x \quad (iv)\; 4u^2 + 8u \quad (v)\; t^2 – 15 \quad (vi)\; 3x^2 – x – 4\)
Answer
\(\quad (i) \; Let \, p (x) = x^2 – 2x – 8 = x^2– 4x+2x–8 = x(x–4)+2(x–4) = (x-4)(x+2)\\
\quad p(x) = 0
\Rightarrow (x-4)(x+2) = 0
\Rightarrow x = 4 or x = -2 \)
\(\quad\)Verify
\(\quad\) Sum of zeroes = 4 + (-2) = \(\frac{2}{1} = \frac{-\text{coefficient of x}}{\text{coefficient of} x^2}\)
\(\quad\) Product of zeros = 4 × (-2) = \(\frac{- 8}{1} = \frac{\text{constant term}}{\text{coefficient of} x^2}\)
\(\quad (ii) \; Let \, p (s) = 4s^2 – 4s + 1 = 4s^2– 2s – 2s + 1 = 2s(2s – 1) – 2(2s – 1) = (2s – 1)(2s – 1)\\
\quad p(x) = 0
\Rightarrow (2s – 1)(2s – 1) = 0
\Rightarrow s = \frac{1}{2} or s = \frac{1}{2} \)
\(\quad\)Verify
\(\quad\)Sum of zeroes = \(\frac{1}{2} + \frac{1}{2} = \frac{4}{4}\) = \(\frac{-\text{coefficient of x}}{\text{coefficient of} x^2}\)
\(\quad\) Product of zeros = \(\frac{1}{2} \times \frac{1}{2} \) = \(\frac{1}{4} = \frac{\text{constant term}}{\text{coefficient of} x^2}\)
\(\quad (iii) \; Let \, p (x) = 6x^2 – 3 – 7x = 6x^2 – 7x – 3 = 6x^2 – 9x + 2x – 3 = 3x(2x – 3) + 1(2x – 3) = (2x – 3)(3x + 1)\\
\quad p(x) = 0
\Rightarrow (2x – 3)(3x + 1) = 0
\Rightarrow x = \frac{3}{2} or x = \frac{-1}{3} \)
\(\quad\)Verify
\(\quad\)Sum of zeroes = \(\frac{3}{2} + \frac{-1}{3} = \frac{7}{6}\) = \(\frac{-\text{coefficient of x}}{\text{coefficient of} x^2}\)
\(\quad\) Product of zeros = \(\frac{3}{2} \times \frac{-1}{3} \) = \(\frac{-3}{6} = \frac{\text{constant term}}{\text{coefficient of} x^2}\)
\(\quad (iv) \; Let \, p (u) = 4u^2 + 8u = 4u(u + 2)\\
\quad p(u) = 0
\Rightarrow 4u(u + 2) = 0
\Rightarrow u = 0 or u = – 2 \)
\(\quad\)Verify
\(\quad\)Sum of zeroes = 0+ (-2) = \(\frac{-2}{1}\) = \(\frac{-\text{coefficient of u}}{\text{coefficient of} u^2}\)
\(\quad\) Product of zeros = \(0 \times (-2) \) = \(\frac{0}{1} = \frac{\text{constant term}}{\text{coefficient of} u^2}\)
\(\quad (v) \; Let \, p (t) = t^2 – 15 = (t)^2 – (\sqrt{15})^2 = (t + \sqrt{15})(t – \sqrt{15})\\
\quad \quad P(t) = 0
\Rightarrow (t + \sqrt{15})(t – \sqrt{15})= 0
\Rightarrow t = – \sqrt{15} or t = \sqrt{15} \)
\(\quad\)Verify
\(\quad\)Sum of zeroes = \(-\sqrt{15} + \sqrt{15} = \frac{0}{1}\) = \(\frac{-\text{coefficient of t}}{\text{coefficient of} t^2}\)
\(\quad\) Product of zeros = \(-\sqrt{15}\times \sqrt{15}\) = -15= \(\frac{\text{constant term}}{\text{coefficient of} t^2}\)
\(\quad (vi) \; Let \, p (x) = 3x^2 – x – 4 = 3x^2 – 4x + 3x – 4 = x(3x – 4) + 1(3x – 4) = (3x – 4)(x + 1)\\
\quad p(x) = 0
\Rightarrow (3x – 4)(x + 1) = 0
\Rightarrow x = \frac{4}{3} or x = -1 \)
\(\quad\)Verify
\(\quad\)Sum of zeroes = \(\frac{4}{3} + (-1) = \frac{1}{3}\) = \(\frac{-\text{coefficient of x}}{\text{coefficient of} x^2}\)
\(\quad\) Product of zeros = \(\frac{4}{3} \times (-1)\) = \(\frac{-4}{3} = \frac{\text{constant term}}{\text{coefficient of} x^2}\)
Question 2:
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
\(\quad (i) \; \frac{1}{4}, – 1 \quad (ii) \; \sqrt{2}, \frac{1}{3} \quad (iii) \; 0, \sqrt{5} \quad (iv) \; 1, 1 \quad (v) \; -\frac{1}{4}, \frac{1}{4}1 \quad (vi) \; 4, 1\)
Answer
\(\quad (i) \frac{1}{4}, – 1 \)
\(\quad \) Sum of zeroes = \(\alpha + \beta\) = 4
\(\quad \)Product of zeroes = \(\alpha \times \beta\) = – 1
\(\quad \)Quadratic Polynomial
\(\quad x^2 – (\alpha + \beta)x + \alpha \times \beta \\
\quad = x^2 – 4x + (-1)\\
\quad = x^2 – 4x – 1 \)
\(\quad (ii) \sqrt{2}, \frac{1}{3}\)
\(\quad \) Sum of zeroes = \(\alpha + \beta = \sqrt{2}\)
\(\quad \)Product of zeroes = \(\alpha \times \beta = \frac{1}{3}\)
\(\quad \)Quadratic Polynomial
\(\quad x^2 – (\alpha + \beta)x + \alpha \times \beta \\
\quad = x^2 – \sqrt{2}x + \frac{1}{3}\\
\quad = 3x^2 – 3\sqrt{2}x + 1\)
\(\quad (iii) 0, \sqrt{5} \)
\(\quad \) Sum of zeroes = \(\alpha + \beta\) = 0
\(\quad \)Product of zeroes = \(\alpha \times \beta = \sqrt{5}\)
\(\quad \)Quadratic Polynomial
\(\quad x^2 – (\alpha + \beta)x + \alpha \times \beta \\
\quad = x^2 – 0x + \sqrt{5}\\
\quad = x^2 + \sqrt{5} \)
\(\quad (iv) \; 1, 1\)
\(\quad \) Sum of zeroes = \(\alpha + \beta\) = 1
\(\quad \)Product of zeroes = \(\alpha \times \beta\) = 1
\(\quad \)Quadratic Polynomial
\(\quad x^2 – (\alpha + \beta)x + \alpha \times \beta \\
\quad = x^2 – 1x + 1\\
\quad = x^2 – x + 1 \)
\(\quad (v) \frac{-1}{4}, \frac{1}{4} \)
\(\quad \) Sum of zeroes = \(\alpha + \beta = \frac{-1}{4}\)
\(\quad \)Product of zeroes = \(\alpha \times \beta = \frac{1}{4}\)
\(\quad \)Quadratic Polynomial
\(\quad x^2 – (\alpha + \beta)x + \alpha \times \beta \\
\quad = x^2 – \frac{-1}{4}x + \frac{1}{4} \\
\quad = 4x^2 + x + 4\)
\(\quad (vi) 4, 1 \)
\(\quad \) Sum of zeroes = \(\alpha + \beta\) = 4
\(\quad \)Product of zeroes = \(\alpha \times \beta\) = 1
\(\quad \)Quadratic Polynomial
\(\quad x^2 – (\alpha + \beta)x + \alpha \times \beta \\
\quad = x^2 – 4x + 1\)

