NCERT Solution of Class 9 Maths Chapter 8 Quadrilaterals
Thank you for reading this post, don't forget to subscribe!
Exercise 8.1 Class 9 Maths Chapter 8 Quadrilaterals
Question 1.
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Solution:
Given:
ABCD is a parallelogram in which AC = DB
To Prove:
ABCD is a rectangle.
Proof:
In ∆ABC and ∆DCB,
AC = DB [Given]
AB = DC [Opposite sides of a parallelogram]
BC = CB [Common]
∴ ∆ABC ≅ ∆DCB [By SSS congruency]
⇒ ∠ABC = ∠DCB [By C.P.C.T.] …(1)
Now, AB || DC and BC is a transversal. [ ∵ ABCD is a parallelogram]
∴ ∠ABC + ∠DCB = 180° … (2) [Co-interior angles]
From (1) and (2),
∠ABC = ∠DCB = 90°
i.e., ABCD is a parallelogram having an angle equal to 90°.
∴ ABCD is a rectangle.
Class 9 Maths Chapter 8 Quadrilaterals
Question 2.
Show that the diagonals of a square are equal and bisect each other at right angles.
Solution:
Given:
ABCD is a square and its diagonals AC and BD intersect at O.
To Prove:
(i) AC = BD
(ii) OA = OC and OD = OB
(iii) ∠AOB = ∠AOD = 90°
Proof:
In ∆ABC and ∆BAD,
AB = BA [Common]
BC = AD [Sides of a square ABCD]
∠ABC = ∠BAD [Each angle is 90°]
∴ ∆ABC ≅ ∆BAD [By SAS congruency]
AC = BD [C.P.C.T.] …(1)
(ii) A square is a parallelogram
In ∆OAD and ∆OCB,
AD = CB [Sides of a square ABCD]
∠ODA = ∠OBC [AD || BC and Alternate interior angles]
∠OAD = ∠OCB [AD || BC and Alternate interior angles]
∴ ∆OAD ≅ ∆OCB [By ASA congruency]
⇒ OA = OC and OD = OB [By C.P.C.T.]
i.e., the diagonals AC and BD bisect each other at O. …….(2)
(iii) In ∆OBA and ∆ODA,
OB = OD [Proved]
BA = DA [Sides of a square ABCD]
OA = OA [Common]
∴ ∆OBA ≅ ∆ODA [By SSS congruency]
⇒ ∠AOB = ∠AOD [By C.P.C.T.] …(3)
∴∠AOB + ∠AOD = 180° [linear pair]
∴∠AOB = ∠AOD = 90° [By(3)]
From (1), (2) and (3), we get AC and BD are equal and bisect each other at right angles.
Class 9 Maths Chapter 8 Quadrilaterals
Question 3.
Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.
Solution
Given:
ABCD is a parallelogram in which diagonal AC bisects ∠A
⇒ ∠DAC = ∠BAC
To Prove:
(i) AC bisects ∠C,
(ii) ABCD is a rhombus.
Proof:
(i) Since, ABCD is a parallelogram.
∴ AB || DC and AC is a transversal.
∴ ∠1 = ∠3 …(1) [Alternate interior angles]
Also, BC || AD and AC is a transversal.
∴ ∠2 = ∠4 …(2) [Alternate interior angles]
Also, ∠1 = ∠2 …(3)
[ ∵ AC bisects ∠A]
From (1), (2) and (3), we have
∠3 = ∠4
⇒ AC bisects ∠C.
(ii) In ∆ABC, we have
∠1 = ∠4 [From (2) and (3)]
⇒ BC = AB …(4)
[ ∵ Sides opposite to equal angles of a ∆ are equal]
Similarly, AD = DC ……..(5)
But, ABCD is a parallelogram. [Given]
∴ AB = DC …(6)
From (4), (5) and (6), we have
AB = BC = CD = DA
Thus, ABCD is a rhombus.
Class 9 Maths Chapter 8 Quadrilaterals
Question 4.
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
(i) ABCD is a square
(ii) diagonal BD bisects ∠B as well as ∠D.
Solution
Given:
ABCD is a rectangle in which AC bisects ∠A as well as ∠C.
i.e., ∠1 = ∠4 and ∠2 = ∠3
To Prove:
(i) ABCD is a square
(ii) Diagonal BD bisects ∠B as well as ∠D.
Proof:
(i) Since, every rectangle is a parallelogram.
∴ ABCD is a parallelogram.
⇒ AB || CD and AC is a transversal.
∴∠2 = ∠4 …(2) [Alternate interior angles]
But ∠2 = ∠3
∠3 = ∠4
In ∆ABC, ∠3 = ∠4
⇒ AB = BC [Sides opposite to equal angles of a A are equal]
Similarly, CD = DA
So, ABCD is a rectangle having adjacent sides equal.
⇒ ABCD is a square.
(ii) Since, ABCD is a square and diagonals of a square bisect the opposite angles.
So, BD bisects ∠B as well as ∠D.
Exercise 8.1 Class 9 Maths Chapter 8 Quadrilaterals
Question 5.
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that
\((i)\quad \triangle APD \cong \triangle CQB \quad (ii)\;AP = CQ \\ (iii) \; \triangle AQB \cong \triangle CPD \quad (iv)\; AQ = CP \\ (v)\; APCQ \,is\,a \,parallelogram.\) [Imp.]
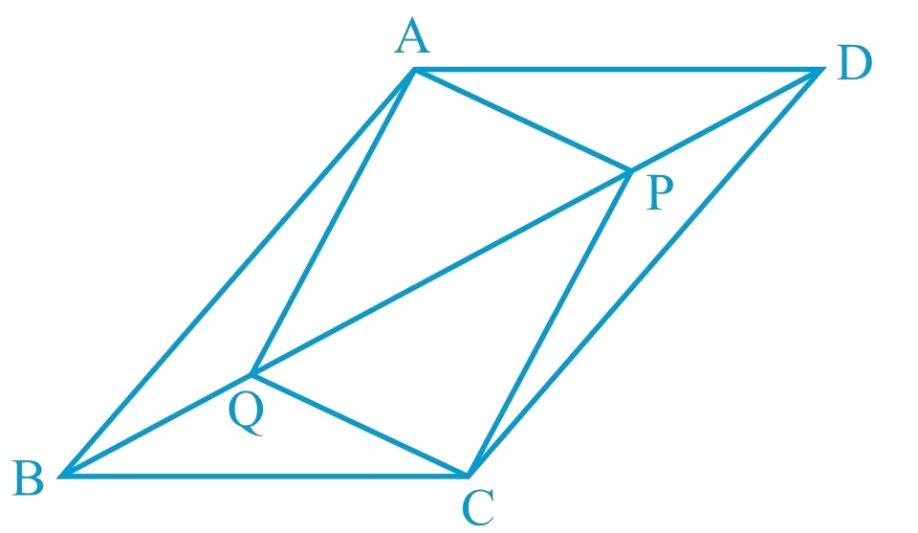
Solution
Given:
A parallelogram ABCD, BD is the diagonal and DP = BQ
(i) Since, AD || BC and BD is a transversal.
∴ ∠ADB = ∠CBD [ Alternate interior angles]
⇒ ∠ADP = ∠CBQ
Now,
In ∆APD and ∆CQB,
AD = CB [Opposite sides of a parallelogram ABCD are equal]
PD = QB [Given]
∠ADP = ∠CBQ [Proved]
∴ ∆APD ≅ ∆CQB [By SAS congruency]
(ii) Since, ∆APD ≅ ∆CQB [Proved]
⇒ AP = CQ [By C.P.C.T.]
(iii) Since, AB || CD and BD is a transversal.
∴ ∠ABD = ∠CDB
⇒ ∠ABQ = ∠CDP
Now,
In ∆AQB and ∆CPD,
QB = PD [Given]
∠ABQ = ∠CDP [Proved]
AB = CD [ Y Opposite sides of a parallelogram ABCD are equal]
∴ ∆AQB = ∆CPD [By SAS congruency]
(iv) Since, ∆AQB = ∆CPD [Proved]
⇒ AQ = CP [By C.P.C.T.]
(v) In a quadrilateral ∆PCQ,
Opposite sides are equal. [Proved]
∴ ∆PCQ is a parallelogram.
Class 9 Maths Chapter 8 Quadrilaterals
Question 6.
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see figure). Show that
Solution
(i) In ∆APB and ∆CQD,
∠APB = ∠CQD [Each 90°]
AB = CD [Opposite sides of a parallelogram ABCD are equal]
∠ABP = ∠CDQ [Alternate angles are equal as AB || CD and BD is a transversal]
∴ ∆APB = ∆CQD [By AAS congruency]
(ii) Since, ∆APB ≅ ∆CQD [Proved]
⇒ AP = CQ [By C.P.C.T.]
Class 9 Maths Chapter 8 Quadrilaterals
Question 7.
ABCD is a trapezium in which AB || CD and AD = BC (see figure). Show that
(i )∠A=∠B
(ii )∠C=∠D
(iii) ∆ABC ≅ ∆BAD
(iv) diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E].
Solution:
Given:
A trapezium ABCD in which AB || CD and AD = BC.
(i) Produce AB to E and draw CE || AD.. .(1)
∵ AB || DC
⇒ AE || DC Also AD || CE
∴ AECD is a parallelogram.
⇒ AD = CE …(1) [Opposite sides of the parallelogram are equal]
But AD = BC …(2) [Given]
By (1) and (2), BC = CF
Now, in ∆BCF, BC = CF
⇒ ∠CEB = ∠CBE …(3) [Angles opposite to equal sides of a triangle are equal]
Also, ∠ABC + ∠CBE = 180° … (4) [Linear pair]
and ∠A + ∠CEB = 180° …(5) [Co-interior angles of a parallelogram ADCE]
From (4) and (5),
∠ABC + ∠CBE = ∠A + ∠CEB
⇒ ∠ABC = ∠A [From (3)]
⇒ ∠B = ∠A …(6)
(ii) AB || CD and AD is a transversal.
∴ ∠A + ∠D = 180° …(7) [Co-interior angles]
Similarly, ∠B + ∠C = 180° … (8)
From (7) and (8),
∠A + ∠D = ∠B + ∠C
⇒ ∠C = ∠D [From (6)]
(iii) In ∆ABC and ∆BAD,
AB = BA [Common]
BC = AD [Given]
∠ABC = ∠BAD [Proved]
∴ ∆ABC = ∆BAD [By SAS congruency]
(iv) Since, ∆ABC = ∆BAD [Proved]
⇒ AC = BD [By C.P.C.T.]
Class 9 Maths Chapter 8 Quadrilaterals
Exercise 8.2 Class 9 Maths Chapter 8 Quadrilaterals
Question 1.
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see figure). AC is a diagonal. Show that
(i) SR || AC and SR = ½AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Solution:
(i) In ∆ACD,
∴ S is the mid-point of AD and R is the mid-point of CD.
SR = ½AC and SR || AC …(1) [By mid-point theorem]
(ii) In ∆ABC, P is the mid-point of AB and Q is the mid-point of BC.
PQ = ½AC and PQ || AC …(2) [By mid-point theorem]
From (1) and (2), we get
PQ = ½AC = SR and PQ || AC || SR
⇒ PQ = SR and PQ || SR
(iii) In a quadrilateral PQRS,
PQ = SR and PQ || SR [Proved]
∴ PQRS is a parallelogram.
Class 9 Maths Chapter 8 Quadrilaterals
Question 2:
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rectangle.
Solution
We have a rhombus ABCD and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Join AC.
In ∆ABC, P and Q are the mid-points of AB and BC respectively.
∴ PQ = ½AC and PQ || AC …(1) [By mid-point theorem]
In ∆ADC, R and S are the mid-points of CD and DA respectively.
∴ SR = ½AC and SR || AC …(2) [By mid-point theorem]
From (1) and (2),
PQ = ½AC = SR and PQ || AC || SR
⇒ PQ = SR and PQ || SR
∴ PQRS is a parallelogram. …….(3)
Now, in ∆ERC and ∆EQC,
∠1 = ∠2 [The diagonals of a rhombus bisect the opposite angles]
CR = CQ [ ∵CD/2 = BC/2]
CE = CE [Common]
∴ ∆ERC ≅ ∆EQC [By SAS congruency]
⇒ ∠3 = ∠4 …(4) [By C.P.C.T.]
But ∠3 + ∠4 = 180° ……(5) [Linear pair]
From (4) and (5), ⇒ ∠3 = ∠4 = 90°
Now, ∠RQP = 180° – ∠5 [ Co-interior angles for PQ || AC and EQ is transversal]
But ∠5 = ∠3 [Vertically opposite angles]
∴ ∠5 = 90°
So, ∠RQP = 180° – ∠5 = 90°
∴ One angle of parallelogram PQRS is 90°.
Thus, PQRS is a rectangle.
Class 9 Maths Chapter 8 Quadrilaterals
Question 3.
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rhombus.
Solution:
In ∆ABC, we have
PQ = ½AC and PQ || AC …(1) [By mid-point theorem]
Similarly, in ∆ADC,
SR = ½AC and SR || AC …(2) [By mid-point theorem]
From (1) and (2), we get
PQ = SR and PQ || SR
∴ PQRS is a parallelogram.
Now, in ∆PAS and ∆PBQ, we have
∠A = ∠B [Each 90°]
AP = BP [ ∵ P is the mid-point of AB]
AS = BQ [∵ ½ AD = ½ BC]
∴ ∆PAS ≅ ∆PBQ [By SAS congruency]
⇒ PS = PQ [By C.P.C.T.]
Also, PS = QR and PQ = SR [∵opposite sides of a parallelogram are equal]
So, PQ = QR = RS = SP i.e., PQRS is a parallelogram having all of its sides equal.
Hence, PQRS is a rhombus.
Class 9 Maths Chapter 8 Quadrilaterals
Question 4.
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see figure). Show that F is the mid-point of BC.
Solution:
We have,
In ∆DAB, E is the mid-point of AD and EG || AB [∵ EF || AB]
Using the converse of mid-point theorem,
we get, G is the mid-point of BD.
Again in ABDC,
we have G is the midpoint of BD and GF || DC.
[∵ AB || DC and EF || AB and GF is a part of EF]
Using the converse of the mid-point theorem,
we get, F is the mid-point of BC.
Class 9 Maths Chapter 8 Quadrilaterals
Question 5.
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see figure). Show that the line segments AF and EC trisect the diagonal BD.
Solution:
Since, the opposite sides of a parallelogram are parallel and equal.
∴ AB || DC
⇒ AE || FC …(1)
and AB = DC
⇒ ½ AB = ½ DC
⇒ AE = FC …(2)
From (1) and (2), we have
AE || PC and AE = PC
∴ ∆ECF is a parallelogram.
Now, in ∆DQC, we have F is the mid-point of DC and FP || CQ
[∵ AF || CE]
⇒ DP = PQ …(3) [By converse of mid-point theorem]
Similarly, in A BAP, E is the mid-point of AB and EQ || AP [∵AF || CE]
⇒ BQ = PQ …(4) [By converse of mid-point theorem]
∴ From (3) and (4), we have
DP = PQ = BQ
So, the line segments AF and EC trisect the diagonal BD.
Class 9 Maths Chapter 8 Quadrilaterals
Question 6:
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = ½AB
Solution:
We have
(i) In ∆ACB, We have
M is the mid-point of AB. [Given]
MD || BC , [Given]
∴ Using the converse of mid-point theorem,
D is the mid-point of AC.
(ii) Since, MD || BC and AC is a transversal.
∠MDA = ∠BCA [ ∵ Corresponding angles are equal]
As ∠BCA = 90° [Given]
∠MDA = 90°
⇒ MD ⊥AC.
(iii) In ∆ADM and ∆CDM, we have
∠ADM = ∠CDM [Each equal to 90°]
MD = MD [Common]
AD = CD [∵ D is the mid-point of AC]
∴ ∆ADM ≅ ∆CDM [By SAS congruency]
⇒ MA = MC [By C.P.C.T.] .. .(1)
∵ M is the mid-point of AB [Given]
MA = ½ AB …(2)
From (1) and (2), we have
CM = MA = ½AB
Class 9 Maths Chapter 8 Quadrilaterals

