NCERT Solutions for Class 10 Maths Chapter 6 Triangles त्रिभुज
Table of Contents
Exercise 6.1
Question 1:
Fill in the blanks using the correct word given in brackets :
(i) All circles are __________. (congruent, similar)
(ii) All squares are __________ . (similar, congruent)
(iii) All __________ triangles are similar. (isosceles, equilateral)
(iv) Two polygons of the same number of sides are similar, if (a) their corresponding angles are __________ and (b) their corresponding sides are __________. (equal, proportional)
कोष्ठकों में दिए शब्दों में से सही शब्दों का प्रयोग करते हुए, रिक्त स्थानों को भरिए :
(i) सभी वृत्त …………. होते है | (सर्वांगसम, समरूप)
(ii) सभी वर्ग …………. होते हैं| (समरूप, सर्वांगसम)
(iv) सभी …………. त्रिभुज समरूप होते है | (समद्विबाहु, समबाहु)
(v) भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि उनके संगत कोण (i) ………… हो तथा उनकी संगत (ii) ………… भुजाएँ हों | (बराबर, समानुपाती)
Solution
(i) similar समरूप
(ii) similar समरूप
(iii) equilateral समबाहु
(iv) (a) eqaul (b) proportional (a) बराबर, (b) समानुपाती
Question 2:
Give two different examples of pair of
(i) similar figures. (ii) non-similar figures.
निम्नलिखित युग्मों के दो भिन्न -भिन्न उदाहरण दीजिए :
(i) समरूप आकृतियाँ
(ii) ऐसी आकृतियाँ जो समरूप नहीं हैं |
Solution
(i) A pair of equilateral triangles of different sides lengths, a pair of two rectangles of different lenghts and breadths, etc.
(ii) A pair of rectangle and a parallelogram with angles not equal to 900, a pair of isosceles triangle and a scalene triangle, etc.
(i) दो वृत्त और दो वर्ग
(ii) वृत्त और वर्ग तथा त्रिभुज और चतुर्भुज
Question 3:
State whether the following quadrilaterals are similar or not:
बताइए की निम्नलिखित चतुर्भुज समरूप है या नहीं :
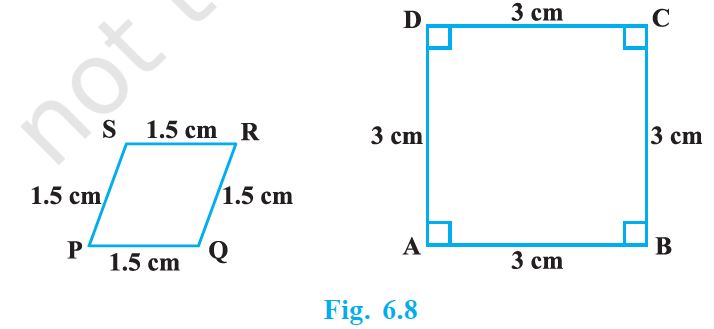
Solution
PQRS and ABCD are not similar.
PQRS and ABCD चतुर्भुज समरूप नहीं है
Exercise 6.2
Question 1:
In Fig. 6.17, (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).
आकृति 6.17 (i) और (ii) में, DE || BC में AD ज्ञात कीजिए :
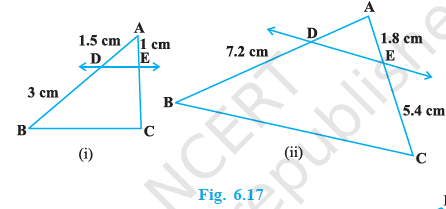
Solution
(i) In △ ABC,
\(\quad\) DE∥BC
\(\quad\)∴ \(\frac{AD}{DB}\) = \(\frac{AE}{EC}\) [Using Basic proportionality theorem]
⇒\(\frac{1.5}{3}\) = \(\frac{1}{EC}\)
⇒EC = 2 cm
(ii) In △ ABC,
\(\quad\)DE∥BC
\(\quad\)∴ \(\frac{AD}{DB}\) = \(\frac{AE}{EC}\) [Using Basic proportionality theorem]
⇒ \(\frac{AD}{7.2}\)= \(\frac{1.8}{5.4}\)
⇒ AD = 2.4 cm.
Question 2:
E and F are points on the sides PQ and PR respectively of a \(\triangle\) PQR. For each of the following cases, state whether EF || QR :
किसी त्रिभुज PQR की भुजाओं PQऔर PR पर क्रमशः बिन्दु E और F स्थित हैं | निम्नलिखित में से प्रत्येक स्थिति के लिए, बताइए कि क्या EF|| QR है |
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Solution
(i) PE = 3.9 cm, EQ= 3cm, PF = 3.6 और FR= 2.4 cm
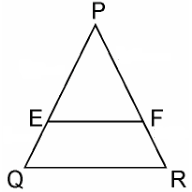
By Basic proportionality theorem,
we get, \(\frac{PE}{EQ}\) = \(\frac{3.9}{3}\) = 1.3 and \(\frac{PF}{FR}\)= \(\frac{3.6}{2.4}\) = 1.5
So, we get, \(\frac{PE}{EQ}\) ≠ \(\frac{PF}{FR}\)
Hence, EF is not parallel to QR.
(ii) Given, PE = 4 cm, QE = 4.5 cm, PF = 8cm and RF = 9cm

By Basic proportionality theorem, we get,
\(\frac{PE}{QE}\) = \(\frac{4}{4.5}\) = \(\frac{8}{9}\) and, \(\frac{PF}{RF}\) = \(\frac{8}{9}\)
So, we get here, \(\frac{PE}{QE}\) = \(\frac{PF}{RF}\)
Hence, EF is parallel to QR.
(iii) Given, PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm

From the figure, EQ = PQ – PE = 1.28 – 0.18 = 1.10 cm and, FR = PR – PF = 2.56 – 0.36 = 2.20 cm
So, \(\frac{PE}{EQ}\) = \(\frac{0.18}{1.10\) = \(\frac{9}{55}\)…………. (i)
and, \(\frac{PF}{FR}\) = \(\frac{0.36}{2.20}\) = \(\frac{9}{55}\) ………… (ii)
So, we get here, PE/EQ = PF/FR
Hence, EF is parallel to QR.
Question 3:
In Fig. 6.18, if LM || CB and LN || CD, prove that \(\frac{AM}{AB}\) = \(\frac{AN}{AD}\).
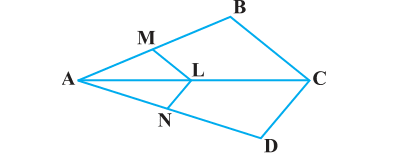
Solution
In the given figure, LM || CB,
By Basic Proportionality Theorem,
we get, \(\frac{AM}{AB}\) = \(\frac{AL}{AC}\)……………………..(i)
Similarly, given, LN || CD and using basic proportionality theorem,
∴\(\frac{AN}{AD}\) = \(\frac{AL}{AC}\) ……………………………(ii)
From equation (i) and (ii) ,
we get, \(\frac{AM}{AB}\) = \(\frac{AN}{AD}\)
Hence, proved.
Question 4:
In Fig. 6.19, DE || AC and DF || AE. Prove that \(\frac{AM}{AB}\) = \(\frac{AN}{AD}\)
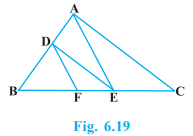
Solution
Question 5:
In Fig. 6.20, DE || OQ and DF || OR. Show that EF || QR.
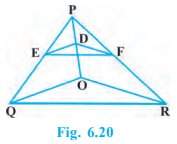
Question 6:
In Fig. 6.21, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
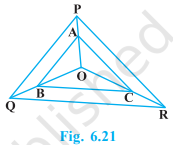
Question 7:
Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
Question 8:
Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX)
Question 9:
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\).
Question 10:
The diagonals of a quadrilateral ABCD intersect each other at the point O such that \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\). Show that ABCD is a trapezium.
NCERT Solutions for Class 10 Maths Chapter 6 Triangles त्रिभुज
Exercise 6.3
Question 1:
State which pairs of triangles in Fig. 6.34 are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :
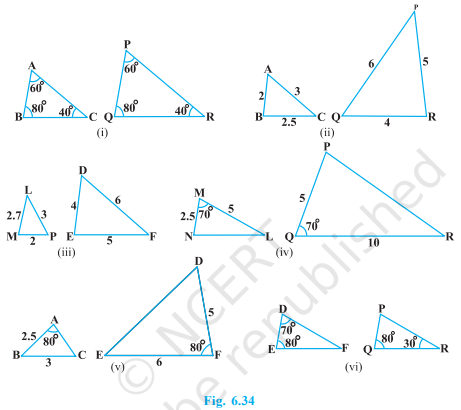
Question 2:
In Fig. 6.35, \(\triangle\) ODC ~ \(\triangle\) OBA, \(\triangle\) BOC = 125° and \(\triangle\) CDO = 70°. Find \(\triangle\) DOC, \(\triangle\) DCO and \(\triangle\) OAB.
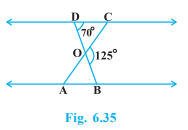
Question 3:
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that \(\frac{OA}{OC}\) = \(\frac{OB}{OD}\).
Question 4:
In Fig. 6.36, \(\frac{QR}{QS}\) = \(\frac{QT}{PR}\) and \(\angle\) 1 = \(\angle\) 2. Show that \(\triangle\) PQS ~ \(\triangle\) TQR.
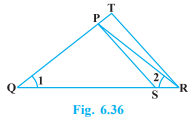
Question 5:
S and T are points on sides PR and QR of \(\triangle\) PQR such that \(\angle\) P = \(\angle\) RTS. Show that \(\triangle\) RPQ ~ \(\triangle\) RTS.
Question 6:
In Fig. 6.37, if \(\Delta ABE \cong \Delta\) ACD, show that \(\triangle\) ADE ~ \(\triangle\) ABC.
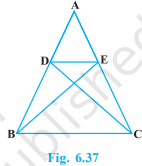
Question 7:
In Fig. 6.38, altitudes AD and CE of \(\Delta\) ABC intersect each other at the point P. Show that:
(i) \(\Delta\) AEP ~ \(\Delta\) CDP
(ii) \(\Delta\) ABD ~ \(\Delta\) CBE
(iii) \(\Delta\) AEP ~ \(\Delta\) ADB
(iv) \(\Delta\) PDC ~ \(\Delta\) BEC
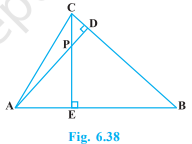
Question 8:
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that \(\Delta\) ABE ~ \(\Delta\) CFB.
Question 9:
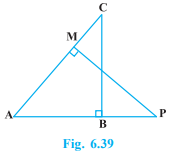
In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:
(i) \(\Delta\) ABC ~ \(\Delta\) AMP
(ii) \(\frac{CA}{PA} = \frac{BC}{MP}\)
Question 10:
CD and GH are respectively the bisectors of \(\Delta\) ACB and \(\Delta\) EGF such that D and H lie on sides AB and FE of \(\Delta\) ABC and \(\Delta\) EFG respectively. If \(\Delta\) ABC ~ \(\Delta\) FEG, show that:
(i) \(\frac{CD}{GH} = \frac{AC}{FG}\)
(ii) \(\Delta\) DCB ~ \(\Delta\) HGE
(iii) \(\Delta\) DCA ~ \(\Delta\) HGF
Question 11:
In Fig. 6.40, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD \(\perp\) BC and EF \(\perp\) AC, prove that \(\Delta\) ABD ~ \(\Delta\) ECF.
Question 12:
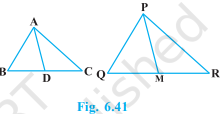
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of \(\Delta\) PQR (see Fig. 6.41). Show that \(\Delta\) ABC ~ \(\Delta\) PQR.
Question 13:
D is a point on the side BC of a triangle ABC such that \(\Delta\) ADC = \(\Delta\) BAC. Show that CA2 = CB.CD.
Question 14:
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that \(\Delta\) ABC ~ \(\Delta\) PQR.
Question 15:
A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Question 16:
If AD and PM are medians of triangles ABC and PQR, respectively where \(\Delta\) ABC ~ \(\Delta\) PQR, prove that
NCERT Solutions for Class 10 Maths Chapter 6 Triangles त्रिभुज

