Class 11 Maths Ch-2 Relations and Functions

NCERT Solutions of Class 11 Maths Ch-2 Relations and Functions

Exercise 2.1

Thank you for reading this post, don't forget to subscribe!

Question 1:
If \((\frac{x}{3} + 1, y – \frac{2}{3}\)) = \((\frac{5}{3}, \frac{1}{3}\)), find the values of x and y.
Answer
\((\frac{x}{3} + 1, y – \frac{2}{3}\)) = \((\frac{5}{3}, \frac{1}{3}\))
\(\Rightarrow \frac{x}{3} + 1 = \frac{5}{3}\) and \(y – \frac{2}{3} = \frac{1}{3}\)
\(\Rightarrow \frac{x}{3} = \frac{5}{3} – 1\) and \(y = \frac{1}{3} + \frac{2}{3}\)
\(\Rightarrow \frac{x}{3} = \frac{2}{3}\) and \(y = \frac{3}{3}\)
\(\Rightarrow\) x = 2 and y = 1

Question 2:
If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in (A×B).
Answer
n(A) = 3 and n(B) = 3
Thus, n(A) × n(B) = 3 × 3 = 9
Hence, the number of elements in (A×B) is 9.

Question 3:
If G = {7, 8} and H = {5, 4, 2}, find G × H and H × G.
Answer
G × H = {7, 8} × {5, 4, 2} = {(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}
H × G = {5, 4, 2} × {7, 8} = {(5, 7), (5, 8), (4, 7), (4, 8), (2, 7), (2, 8)}

Question 4:
State whether each of the following statements are true or false. If the statement is false, rewrite the given statement correctly.
(i) If P = {m, n} and Q = { n, m}, then P × Q = {(m, n),(n, m)}.
(ii) If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that x ∈ A and y ∈ B.
(iii) If A = {1, 2}, B = {3, 4}, then A × (B ∩ φ) = φ.
Answer
(i) False, P × Q = {(m, n), (m, m), (n, n), (n, m)}
(ii) True
(iii) True

Question 5:
If A = {–1, 1}, find A × A × A.
Answer
A × A × A = {–1, 1} × {–1, 1} × {–1, 1} = {(–1, -1, -1), (–1, -1, 1), (–1, 1, 1), (1, -1, 1), (1, 1, -1), (1, -1, -1), (–1, 1, -1), (1, 1, 1)}

Question 6:
If A × B = {(a, x),(a , y), (b, x), (b, y)}. Find A and B.
Answer
A × B = {(a, x),(a , y), (b, x), (b, y)}
A = {a, b} and B = {x, y}

Question 7:
Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that
(i) A × (B ∩ C) = (A × B) ∩ (A × C). (ii) A × C is a subset of B × D.
Answer
B ∩ C = \(\phi\) and A × B = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)}
and A × C = {(1, 5), (1, 6), (2, 5), (2, 6)}
LHS = A × (B ∩ C)
= A = {1, 2} × \(\phi\) = \(\phi\)
RHS = (A × B) ∩ (A × C)
= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)} ∩ {(1, 5), (1, 6), (2, 5), (2, 6)}
= \(\phi\)
Hence, A × (B ∩ C) = (A × B) ∩ (A × C)

Question 8:
Let A = {1, 2} and B = {3, 4}. Write A × B. How many subsets will A × B have? List them.
Answer
A × B = {(1, 3), (1, 4), (2, 3), (2, 4)}
Number of subset A × B = 2⁴ = 16.

Question 9:
Let A and B be two sets such that n(A) = 3 and n(B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y and z are distinct elements.
Answer
n(A) = 3 and n(B) = 2.
A × B = {(x, 1), (y, 2), (z, 1)}
A = {x, y, z} and B = {1, 2}

Question 10:
The Cartesian product A × A has 9 elements among which are found (–1, 0) and (0,1). Find the set A and the remaining elements of A × A.
Answer
We know that, If n(A) = p and n(B) = q, then n(A × B) = pq.
Given,
n(A × A) = 9
So, n(A) × n(A) = 9
Thus, n(A) = 3
As n(A) = 3, clearly A = {–1, 0, 1}
Hence, the remaining elements of set A × A are as follows:
(–1, –1), (–1, 1), (0, –1), (0, 0), (1, –1), (1, 0), and (1, 1)

---

NCERT Solutions of Class 11 Maths Ch-2 Relations and Functions

---

Exercise 2.2

Question 1:
Let A = {1, 2, 3,…,14}. Define a relation R from A to A by R = {(x, y) : 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and range.
Answer
The relation R from A to A is given as:
R = {(x, y): 3x – y = 0, where x, y ∈ A} = {(x, y): 3x = y, where x, y ∈ A}
So,
R = {(1, 3), (2, 6), (3, 9), (4, 12)}
Domain of R = {1, 2, 3, 4}
Codomain of R = A = {1, 2, 3, …, 14}
Range of R = {3, 6, 9, 12}

Question 2:
Define a relation R on the set N of natural numbers by R = {(x, y) : y = x + 5, x is a natural number less than 4; x, y ∈N}. Depict this relationship using roster form. Write down the domain and the range.
Answer
The relation R is given by:
R = {(x, y): y = x + 5, x is a natural number less than 4, x, y ∈ N}
R = {(1, 6), (2, 7), (3, 8)}
Domain of R = {1, 2, 3}
Range of R = {6, 7, 8}

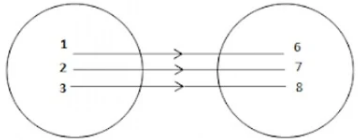
Question 3:
A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}. Write R in roster form.
Answer
A = {1, 2, 3, 5} and B = {4, 6, 9}.
R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}
R = {(1, 4), (1, 6), (2, 9), (3, 4), (3, 6), (5, 4), (5, 6)}

Question 4:
The Fig2.7 shows a relationship between the sets P and Q. Write this relation
(i) in set-builder form (ii) roster form. What is its domain and range?

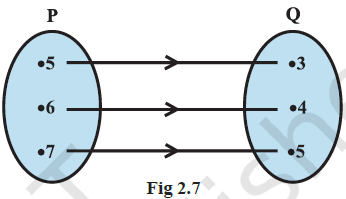
Answer
P = {5, 6, 7} and Q = {3, 4, 5}
(i) R = {(x, y) : y = x – 2; \(x \in P\), \(y \in Q\) }
(ii) R = {(5, 3), (6, 4), (7, 5)}
Domain of R = {5, 6, 7}
Range of R = {3, 4, 5}

Question 5:
Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a , b ∈A, b is exactly divisible by a}.
(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R.
Answer
A = {1, 2, 3, 4, 6} and R = {(a, b): a , b ∈A, b is exactly divisible by a}
(i) R= {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}
(ii) Domain of R = {1, 2, 3, 4, 6}
(iii) Range of R = {1, 2, 3, 4, 6}

Question 6:
Determine the domain and range of the relation R defined by R = {(x, x + 5) : x ∈ {0, 1, 2, 3, 4, 5}}.
Answer
R = {(x, x + 5) : x ∈ {0, 1, 2, 3, 4, 5}}
R = {(0, 5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)}
Domain of R = {0, 1, 2, 3, 4, 5}
Range of R = {5, 6, 7, 8, 9, 10}

Question 7:
Write the relation R = {(x, x³) : x is a prime number less than 10} in roster form.
Answer
R = {(x, x³) : x is a prime number less than 10}
R = {(2, 8), (3, 27), (5, 125), (7, 343)}

Question 8:
Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B.
Answer
A = {x, y, z} and B = {1, 2}
A × B = {(x, 1), (x, 2), (y, 1), (y, 2), (z, 1), (z, 2)}
Since, n(A × B) = 6, the number of subsets of A × B is 2⁶.
So, the number of relations from A to B is 2⁶.

Question 9:
Let R be the relation on Z defined by R = {(a,b): a, b ∈ Z, a – b is an integer}. Find the domain and range of R.
Answer
R = {(a,b): a, b ∈ Z, a – b is an integer}
We know that the difference between any two integers is always an integer.
∴ Domain of R = Z
and, Range of R = Z

---

NCERT Solutions of Class 11 Maths Ch-2 Relations and Functions

---

Exercise 2.3

Question 1:

---

NCERT Solutions of Class 11 Maths Ch-2 Relations and Functions

---

Miscellaneous Exercise on Chapter 2

Question 1:
The relation f is defined by \(f(x) = \begin{cases}
x^2, & 0 \leq x \leq 3 \\
3x, & 3 \leq x \leq 10
\end{cases}\)
The relation g is defined by \(g(x) = \begin{cases}
x^2, & 0 \leq x \leq 2 \\
3x, & 2 \leq x \leq 10
\end{cases}\)
Show that f is a function and g is not a function.
Answer

Question 2:
If f (x) = \(x^2\), find \(\frac{f(1.1) – f(1)}{(1.1 – 1)}\).

Question 3:
Find the domain of the function f (x) = \(\frac{x^2 + 2x + 1}{x^2 – 8x + 12}\).

Question 4:
Find the domain and the range of the real function f defined by \(f(x) = \sqrt{(x – 1)}\).

Question 5:
Find the domain and the range of the real function f defined by f(x) = |x – 1|.

Question 6:
Let be a function from R into R. Determine the range of f.

Question 7:

---

NCERT Solutions of Class 11 Maths Ch-2 Relations and Functions

---