NCERT Solutions of Class 11 Maths Ch-9 Straight Lines
Exercise 9.1
Thank you for reading this post, don't forget to subscribe!Question 1:
Draw a quadrilateral in the Cartesian plane, whose vertices are (– 4, 5), (0, 7), (5, – 5) and (– 4, –2). Also, find its area.
Question 2:
The base of an equilateral triangle with side 2a lies along the y-axis such that the mid-point of the base is at the origin. Find vertices of the triangle.
Question 3:
Find the distance between P (x1, y1) and Q (x2, y2) when : (i) PQ is parallel to the y-axis, (ii) PQ is parallel to the x-axis.
Question 4:
Find a point on the x-axis, which is equidistant from the points (7, 6) and (3, 4).
Question 5:
Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P (0, – 4) and B (8, 0).
Question 6:
Without using the Pythagoras theorem, show that the points (4, 4), (3, 5) and (–1, –1) are the vertices of a right angled triangle.
Question 7:
Find the slope of the line, which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
Question 8:
Without using distance formula, show that points (– 2, – 1), (4, 0), (3, 3) and (–3, 2) are the vertices of a parallelogram.
Question 9:
Find the angle between the x-axis and the line joining the points (3,–1) and (4,–2).
Question 10:
The slope of a line is double of the slope of another line. If tangent of the angle between them is \(\frac{1}{3}/), find the slopes of the lines.
Question 11:
A line passes through (x1, y1) and (h, k). If slope of the line is m, show that k – y1 = m (h – x1).
Exercise 9.2
In Exercises 1 to 8, find the equation of the line which satisfy the given conditions:
Question 1:
Write the equations for the x-and y-axes.
Question 2:
Passing through the point (– 4, 3) with slope \(\frac{1}{2}).
Question 3:
Passing through (0, 0) with slope m.
Question 4:
Passing through (2, 2 3)and inclined with the x-axis at an angle of 75o.
Question 5:
Intersecting the x-axis at a distance of 3 units to the left of origin with slope –2.
Question 6:
Intersecting the y-axis at a distance of 2 units above the origin and making an angle of 30o with positive direction of the x-axis.
Question 7:
Passing through the points (–1, 1) and (2, – 4).
Question 8:
The vertices of Δ PQR are P (2, 1), Q (–2, 3) and R (4, 5). Find equation of the median through the vertex R.
Question 9:
Find the equation of the line passing through (–3, 5) and perpendicular to the line through the points (2, 5) and (–3, 6).
Question 10:
A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1: n. Find the equation of the line.
Question 11:
Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point (2, 3).
Question 12:
Find equation of the line passing through the point (2, 2) and cutting off intercepts on the axes whose sum is 9.
Question 13:
Find equation of the line through the point (0, 2) making an angle \(\frac{2π}{3}) with the positive x-axis. Also, find the equation of line parallel to it and crossing the y-axis at a distance of 2 units below the origin.
Question 14:
The perpendicular from the origin to a line meets it at the point (–2, 9), find theequation of the line.
Question 15:
The length L (in centimetre) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L= 125.134 when C = 110, express L in terms of C.
Question 16:
The owner of a milk store finds that, he can sell 980 litres of milk each week at Rs 14/litre and 1220 litres of milk each week at Rs 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell
weekly at Rs 17/litre?
Question 17:
P (a, b) is the mid-point of a line segment between axes. Show that equation of the line is \(\frac{x}{a} + \frac{y}{b} = 2\).
Question 18:
Point R (h, k) divides a line segment between the axes in the ratio 1: 2. Find equation of the line.
Question 19:
By using the concept of equation of a line, prove that the three points (3, 0), (– 2, – 2) and (8, 2) are collinear.
Exercise 9.3
Question 1:
Reduce the following equations into slope – intercept form and find their slopes and the y – intercepts.
(i) x + 7y = 0, (ii) 6x + 3y – 5 = 0, (iii) y = 0.
Question 2:
Reduce the following equations into intercept form and find their intercepts on the axes.
(i) 3x + 2y – 12 = 0, (ii) 4x – 3y = 6, (iii) 3y + 2 = 0.
Question 3:
Find the distance of the point (–1, 1) from the line 12(x + 6) = 5(y – 2).
Question 4:
Find the points on the x-axis, whose distances from the line \(\frac{x}{3} + \frac{y}{4} = 1\) are 4 units.
Question 5:
Find the distance between parallel lines
(i) 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0 (ii) l (x + y) + p = 0 and l (x + y) – r = 0.
Question 6:
Find equation of the line parallel to the line 3x − 4y + 2 = 0 and passing through the point (–2, 3).
Question 7:
Find equation of the line perpendicular to the line x – 7y + 5 = 0 and having x intercept 3.
Question 8:
Find angles between the lines 3x + y = 1and x + 3y = 1.
Question 9:
The line through the points (h, 3) and (4, 1) intersects the line 7x – 9y -19 = 0. at right angle. Find the value of h.
Question 10:
Prove that the line through the point (x1, y1) and parallel to the line Ax + By + C = 0 is A (x –x1) + B (y – y1) = 0.
Question 11:
Two lines passing through the point (2, 3) intersects each other at an angle of 60o. If slope of one line is 2, find equation of the other line.
Question 12:
Find the equation of the right bisector of the line segment joining the points (3, 4) and (–1, 2).
Question 13:
Find the coordinates of the foot of perpendicular from the point (–1, 3) to the line 3x – 4y – 16 = 0.
Question 14:
The perpendicular from the origin to the line y = mx + c meets it at the point (–1, 2). Find the values of m and c.
Question 15:
If p and q are the lengths of perpendiculars from the origin to the lines x cosθ − ysin θ = k cos 2θ and x sec θ + y cosec θ = k, respectively, prove that p2 + 4q2 = k2.
Question 16:
In the triangle ABC with vertices A (2, 3), B (4, –1) and C (1, 2), find the equation and length of altitude from the vertex A.
Question 17:
If p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that \(\frac{1}{p^2} = \frac{1}{a^2} + \frac{1}{b^2}\).
Miscellaneous Exercise on Chapter 9
Question 1:
Find the values of k for which the line (k–3) x – (4 – k2) y + k2 –7k + 6 = 0 is
(a) Parallel to the x-axis,
(b) Parallel to the y-axis,
(c) Passing through the origin.
Question 2:
Find the equations of the lines, which cut-off intercepts on the axes whose sum and product are 1 and – 6, respectively.
Question 3:
What are the points on the y-axis whose distance from the line \(\frac{x}{3} + \frac{y}{4} = 1\) is 4 units.
Question 4:
Find perpendicular distance from the origin to the line joining the points (cosθ, sin θ) and (cos φ, sin φ).
Question 5:
Find the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x – 7y + 5 = 0 and 3x + y = 0.
Question 6:
Find the equation of a line drawn perpendicular to the line \(\frac{x}{4} + \frac{y}{6} = 1\) through the point, where it meets the y-axis.
Question 7:
Find the area of the triangle formed by the lines y – x = 0, x + y = 0 and x – k = 0.
Question 8:
Find the value of p so that the three lines 3x + y – 2 = 0, px + 2 y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point.
Question 9:
If three lines whose equations are y = m1x + c1, y = m2x + c2 and y = m3x + c3 are concurrent, then show that m1(c2 – c3) + m2 (c3 – c1) + m3 (c1 – c2) = 0.
Question 10:
Find the equation of the lines through the point (3, 2) which make an angle of 45o with the line x – 2y = 3.
Question 11:
Find the equation of the line passing through the point of intersection of the lines 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0 that has equal intercepts on the axes.
Question 12:
Show that the equation of the line passing through the origin and making an angle θ with the line y = mx + c is \(\frac{y}{x} = \frac{m\pm tan}{1\mp mtan}).
Question 13:
In what ratio, the line joining (–1, 1) and (5, 7) is divided by the line x + y = 4?
Question 14:
Find the distance of the line 4x + 7y + 5 = 0 from the point (1, 2) along the line 2x – y = 0.
Question 15:
Find the direction in which a straight line must be drawn through the point (–1, 2) so that its point of intersection with the line x + y = 4 may be at a distance of 3 units from this point.
Question 16:
The hypotenuse of a right angled triangle has its ends at the points (1, 3) and (– 4, 1). Find an equation of the legs (perpendicular sides) of the triangle which are parallel to the axes.
Question 17:
Find the image of the point (3, 8) with respect to the line x +3y = 7 assuming the line to be a plane mirror. [Imp.]
Answer
Let Q (a, b) is the image of the point P (3, 8) in the line
x + 3y = 7 … (1)
Therefore, the line (1) is the perpendicular bisector of line segment AB.
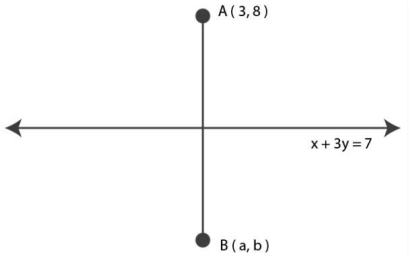
So, \(slope of line AB\times\ {Slope of line (x + 3y = 7)} = 1\),
\(\Rightarrow \frac{b-8}{a-3} \times (\frac{-1}{3}) = 1\)
\(\Rightarrow\) b- 8 = 3a – 9
\(\Rightarrow\) 3a – b = 1 …(2)
We Know that
Mid-point of AB = \((\frac{a + 3}{2},\frac{b + 8}{2})\)
So, the mid-point of the line segment AB will satisfy line (1)
From equation (1),
\((\frac{a + 3}{2}) + 3\frac{b + 8}{2}) = 7\)
\(\Rightarrow\) a + 3 + 3b + 24 = 14
\(\Rightarrow\) a + 3b = – 13 …(3)
Solving (2) and (3),
a = -1 and b = – 4
Hence, the image of the given point is (-1, -4).
Question 18:
If the lines y = 3x +1 and 2y = x + 3 are equally inclined to the line y = mx + 4, find the value of m.
Question 19:
If sum of the perpendicular distances of a variable point P (x, y) from the lines x + y – 5 = 0 and 3x – 2y +7 = 0 is always 10. Show that P must move on a line.
Question 20:
Find equation of the line which is equidistant from parallel lines 9x + 6y – 7 = 0 and 3x + 2y + 6 = 0.
Question 21:
A ray of light passing through the point (1, 2) reflects on the x-axis at point A and the reflected ray passes through the point (5, 3). Find the coordinates of A.
Question 22:
Prove that the product of the lengths of the perpendiculars drawn from the points \((\sqrt{a^2 – b^2}, 0) and -(\sqrt{a^2 – b^2}, 0)\) to the line
Question 23:
A person standing at the junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 wants to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find equation of the path that he should follow.

