NCERT Solutions of Class 9 Maths Chapter 7 Triangles
Table of Contents
Exercise 7.1
Question 1:
In quadrilateral ACBD, AC = AD and AB bisects ∠ A (see Fig. 7.16). Show that Δ ABC ≅ Δ ABD. What can you say about BC and BD?
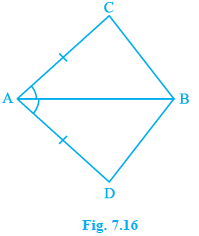
Solution
In Δ ABC and Δ ABD,
AC = AD (Given)
∠CAB = ∠DAB (AB bisects \(\angle A\))
and AB = AB (Common)
Δ ABC ≅ Δ ABD (SAS)
BC = BD
Question 2:
ABCD is a quadrilateral in which AD = BC and ∠ DAB = ∠ CBA (see Fig. 7.17). Prove that
(i) Δ ABD ≅ Δ BAC
(ii) BD = AC
(iii) ∠ ABD = ∠ BAC.
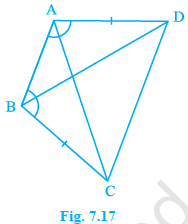
Solution
(i) In Δ ABD and Δ BAC,
\(\quad\) AD = BC [Given]
\(\quad\) ∠DAB = ∠CBA [Given]
\(\quad\) AB = AB [Common]
\(\quad\)Δ ABD ≅ Δ BAC [By SAS congruency]
(ii)Since )Δ ABD ≅ Δ BAC
BD = AC [By C.P.C.T.]
(iii)Since )Δ ABD ≅ Δ BAC
∠ABD = ∠BAC [By C.P.C.T.]
Question 3:
AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.
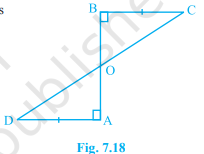
Solution
In Δ BOC and Δ AOD,
∠OBC = ∠OAD [= 90o]
∠BOC = ∠AOD [Vertically Opposite angles]
BC = AD [Given]
Δ BOC ≅ Δ AOD [By ASA congruency]
OB = OA and OC = OD [By C.P.C.T.]
Question 4:
l and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig. 7.19). Show that Δ ABC ≅ Δ CDA.
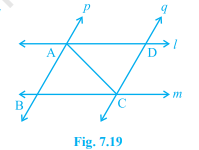
Sollution
In Δ ABC and Δ ADC,
∠ ACB = ∠ DAC [Alternate Interior Angles]
∠ BAC = ∠ ACD [Alternate Interior Angles]
AC = AC [Common]
Δ ABC ≅ Δ CDA [By ASA congruency]
Question 5:
Line l is the bisector of an angle ∠ A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠ A (see Fig. 7.20). Show that:
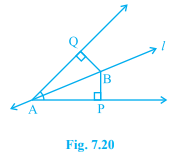
(i) Δ APB ≅ Δ AQB
(ii) BP = BQ or B is equidistant from the arms of ∠ A.
Solution
Line l bisects ∠A.
∠BAP = ∠BAQ … (i)
(i) In Δ ABP and Δ ABQ,
∠BAP = ∠BAQ [from (i)]
∠BPA = ∠BQA [90o]
AB = AB [Common]
Δ APB ≅ Δ AQB [By ASA congruency]
(ii) Since Δ APB ≅ Δ AQB
BP = BQ [By C.P.C.T.]
B is equidistant from the arms of A.
Question 6:
In Fig. 7.21, AC = AE, AB = AD and ∠ BAD = ∠ EAC. Show that BC = DE.
Solution
Question 7:
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠ BAD = ∠ ABE and ∠ EPA = ∠ DPB (see Fig. 7.22). Show that
(i) Δ DAP ≅ Δ EBP
(ii) AD = BE
Solution
Question 8:
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) Δ AMC ≅ Δ BMD
(ii) ∠ DBC is a right angle.
(iii) Δ DBC ≅ Δ ACB
(iv) CM = \(\frac{1}{2}\) AB
NCERT Solutions of Class 9 Maths Chapter 7 Triangles
Exercise 7.2
Question 1:
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠ B and ∠ C intersect each other at O. Join A to O. Show that : (i) OB = OC (ii) AO bisects ∠ A. [Imp.]
Question 2:
In Δ ABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that Δ ABC is an isosceles triangle in which AB = AC.
Question 3:
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
Question 4:
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) Δ ABE ≅ Δ ACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
Question 5:
ABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that ∠ ABD = ∠ ACD.
Question 6:
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig. 7.34). Show that ∠ BCD is a right angle.
Question 7:
ABC is a right angled triangle in which ∠ A = 90° and AB = AC. Find ∠ B and ∠ C. [Imp.]
Question 8:
Show that the angles of an equilateral triangle are 60° each. [Imp.]
Solution
NCERT Solutions of Class 9 Maths Chapter 7 Triangles
Exercise 7.3
Question 1:
Δ ABC and Δ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that
(i) Δ ABD ≅ Δ ACD
(ii) Δ ABP ≅ Δ ACP
(iii) AP bisects ∠ A as well as ∠ D.
(iv) AP is the perpendicular bisector of BC.
Question 2:
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that (i) AD bisects BC (ii) AD bisects ∠ A.
Question 3:
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of Δ PQR (see Fig. 7.40). Show that: [Imp.]
(i) Δ ABM ≅ Δ PQN
(ii) Δ ABC ≅ Δ PQR
Question 4:
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Question 5:
ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠ B = ∠ C.
NCERT Solutions of Class 9 Maths Chapter 7 Triangles

