NCERT Solutions for Class 10 Maths Chapter 9 Some Application of Trigonometry त्रिकोणमिति के कुछ अनुप्रयोग
Important Questions for Class 10 Maths Chapter 9
Thank you for reading this post, don't forget to subscribe!
Exercise 9.1
Question 1:
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° (see Fig. 9.11).
सर्कस का एक कलाकार एक 20 m लंबी डोर पर चढ़ रहा है जो अच्छी तरह से तनी हुई है और भूमि पर सीधे लगे खंभे के शिखर से बंध हुआ है। यदि भूमि स्तर के साथ डोर द्वारा बनाया गया कोण 30° का हो तो खंभे की ऊँचाई ज्ञात कीजिए (देखिए आकृति)|
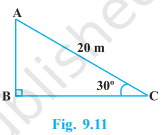
Solution
In \(\triangle\)ABC,
\(\frac{AB}{AC} = \sin \theta \)
\(\Rightarrow \frac{AB}{20} = \sin 30^\circ\)
\(\Rightarrow \frac{AB}{20} = \frac{1}{2}\)
\(\Rightarrow AB = \frac{20}{2} = 10 m\)
Question 2:
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 30० का कोण बनाता है। पेड़ के पाद-बिंदु की दूरी, जहाँ पेड़ का शिखर जमीन को छूता है, 8 m है। पेड़ की ऊँचाई ज्ञात कीजिए।
Solution
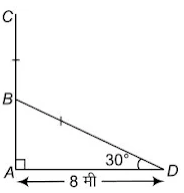
Let AB = x m and BC = y m = BD
In \(\triangle\)BAC,
\(\frac{AB}{AD} = \tan \theta \)
\(\Rightarrow \frac{AB}{8} = \tan 30^\circ\)
\(\Rightarrow \frac{AB}{8} = \frac{1}{\sqrt{3}}\)
\(\Rightarrow AB = \frac{8}{\sqrt{3}}\)
Agian, In \(\triangle\)BAC,
\(\frac{AD}{BD} = \cos \theta \)
\(\Rightarrow \frac{8}{BD} = \cos 30^\circ\)
\(\Rightarrow \frac{8}{BD} = \frac{\sqrt{3}}{2}\)
\(\Rightarrow BD = \frac{16}{\sqrt{3}}\)
Height of the tree, AC = AB + BD
\(\quad\quad\quad\quad\quad\quad\quad\) = \(\frac{8}{\sqrt{3}} + \frac{16}{\sqrt{3}} = \frac{24}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
\(\quad\quad\quad\quad\quad\quad\quad\) = \(\frac{24 \sqrt{3}}{3} = 8\sqrt{3}\)
Question 3:
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
एक ठेकेदार बच्चों को खेलने के लिए एक पार्क में दो फिसलनपट्टी लगाना चाहती है। 5 वर्ष से कम उम्र के बच्चों के लिए वह एक ऐसी फिसलनपट्टी लगाना चाहती है जिसका शिखर 1.5 m की ऊँचाई पर हो और भूमि के साथ 30° के कोण पर झुका हुआ हो, जबकि इससे अधिक उम्र के बच्चों के लिए वह 3 m की ऊँचाई पर एक अधिक ढाल की फिसलनपट्टी लगाना चाहती है, जो भूमि के साथ 60° का कोण बनाती हो। प्रत्येक स्थिति में फिसलनपट्टी की लंबाई क्या होनी चाहिए?
Answer
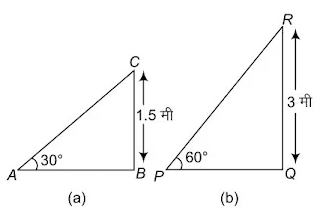
In ΔABC,
sin 30° = \(\frac{BC}{AC}\)
⇒ \(\frac{1}{2}\) = \(\frac{1.5}{AC}\)
⇒ AC = 3 m
In ΔPQR,
sin 60° = \(\frac{QR}{PR}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{3}{PR}\)
⇒ PR = \(\frac{6}{\sqrt{3}}\) = 2\(\sqrt{3}\)m
Question 4:
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
भूमि के एक बिंदु से, जो मीनार के पाद-बिंदु से मी की दूरी पर है, यदि मीनार के शिखर का उन्नयन कोण 30° है तो, मीनार की ऊँचाई ज्ञात कीजिए |
Solution
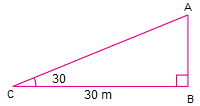
In right ΔABC,
tan 30° = \(\frac{AB}{BC}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{AB}{30}\)
\(\;\\\)
⇒ AB = \(\frac{30}{\sqrt{3}}\) = 10√3
Thus, the height of the tower is 10√3 m.
Question 5:
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
भूमि से 60 m की ऊँचाई पर एक पतंग उड़ रही है। पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिंदु से बांध् दिया गया है। भूमि के साथ डोरी का झुकाव 60° है। यह मानकर कि डोरी में कोई ढील नहीं है, डोरी की लंबाई ज्ञात कीजिए।
Solution
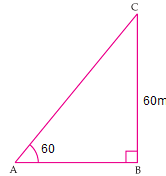
In right ΔABC,
sin 60° = \(\frac{BC}{AC}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{60}{AC}\)
⇒ AC = 40√3 m
Thus, the length of the string from the ground is 40√3 m.
Question 6:
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
1.5 m लंबा एक लड़का 30 m ऊँचे एक भवन से कुछ दूरी पर खड़ा है। जब वह ऊँचे भवन की ओर जाता है तब उसकी आँख से भवन के शिखर का उन्नयन कोण 30° से 60° हो जाता है। बताइए कि वह भवन की ओर कितनी दूरी तक चलकर गया है।
Solution
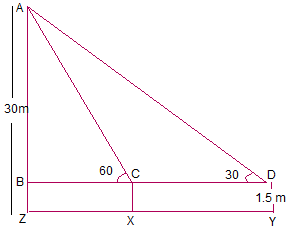
Height of the building = AZ = 30 m
AB = AZ – BZ = (30 – 1.5) = 28.5 m
Let BC = x m and CD = y m
In right ΔABC,
tan 60° = \(\frac{AB}{BC}\)
⇒ √3 = \(\frac{28.5}{x}\)
⇒ x = \(\frac{28.5}{√3}\) = \(\frac{28.5√3}{3}\) = 9.5 \(\sqrt{3}\)
Also, In right ΔABD,
tan 30° = \(\frac{AB}{BD}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{28.5}{x + y}\)
⇒ x + y = 28.5√3 m
⇒ 9.5 \(\sqrt{3}\) + y = 28.5√3 m
⇒ y = 28.5√3 – 9.5 \(\sqrt{3}\) = 19√3
\(\\\)Thus, the distance boy walked towards the building is 19√3 m.
Question 7:
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
भूमि के एक बिंदु से एक 20 m ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमशः 45° और 60° है। मीनार की ऊँचाई ज्ञात कीजिए।
Solution
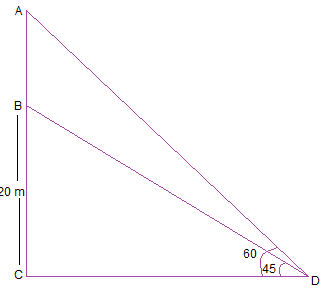
Let AB = x m
In right ΔBCD,
tan 45° = \(\frac{BC}{CD}\)
⇒ 1 = \(\frac{20}{CD}\)
⇒ CD = 20 m
Also, In right ΔACD,
tan 60° = \(\frac{AC}{CD}\)
⇒ √3 = \(\frac{x + 20}{20}\)
⇒ x + 20 = 20√3
⇒ x = 20√3 – 20 = 20(√3 – 1) m
Height of transmission tower = AB = 20(√3 – 1) m.
Question 8:
A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
एक पेडस्टल के शिखर पर एक 1.6 m ऊँची मूर्ति लगी है। भूमि के एक बिंदु से मूर्ति के शिखर का उन्नयन कोण 60° है और उसी बिंदु से पेडस्टल के शिखर का उन्नयन कोण 45° है। पेडस्टल की ऊँचाई ज्ञात कीजिए।
Solution
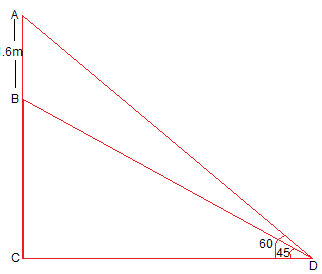
Let AB be the height of statue.
Let height of pedestal = BC = h m and CD = x m
In right ΔBCD,
tan 45° = \(\frac{BC}{CD}\)
⇒ 1 = \(\frac{h}{x}\)
⇒ h = x.
Also, In right ΔACD,
tan 60° = \(\frac{AC}{CD}\)
⇒ √3 = \(\frac{1.6 + h}{x}\)
⇒ √3x = 1.6 + h
⇒ √3h = 1.6 + h
⇒ √3h – h = 1.6
⇒ h(√3-1) = 1.6
⇒ h = \(\frac{1.6}{\sqrt{3} – 1}\)
⇒ h = 0.8(√3+1) m
Thus, the height of the pedestal is 0.8(√3+1) m.
Question 9:
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
एक मीनार के पाद-बिंदु से एक भवन के शिखर का उन्नयन कोण 30o है और भवन के पाद-बिंदु से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50m ऊँची हो, तो भवन की ऊँचाई ज्ञात कीजिए।
Solution
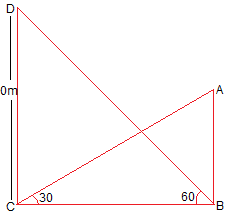
Let AB be h m
In ΔDCB,
\(\frac{DC}{BC}\) = tan 60º
\(\frac{50}{BC}\) = √3
BC = \(\frac{50}{√3}\)
In ΔABC,
\(\frac{AB}{BC}\) = tan 30º
\(\frac{h}{\frac{50}{√3}}\) = \(\frac{1}{√3}\)
h = \(\frac{50}{√3} \times \frac{1}{√3}\) = \(\frac{50}{3}\) = 16\(\frac{2}{3}\)
Therefore, the height of the building is 16\(\frac{2}{3}\) m.
Question 10:
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.
एक 80 m चैड़ी सड़क के दोनों ओर आमने-सामने समान लंबाई वाले दो खंभे लगे हुए हैं। इन दोनों खंभों के बीच सड़क के एक बिंदु से खंभों के शिखर के उन्नयन कोण क्रमशः 60° और 30° है। खंभों की ऊँचाई और खंभों से बिंदु की दूरी ज्ञात कीजिए।
Solution
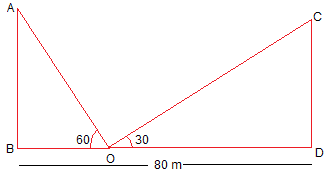
Let AB = CD = h m and BO = x m, DO = (80 – x) m
In ΔABO
\(\frac{AB}{BO}\) = tan 60º
\(\frac{h}{x}\) = √3
h = x √3 …. (1)
In ΔCDO,
\(\frac{CD}{DO}\) = tan 30º
\(\frac{h}{80 – x}\) = \(\frac{1}{\sqrt{3}}\)
h√3 = 80 – x
x √3\(\times\) √3 = 80 – x
3x + x = 80
4x= 80
x = 20
Putting the value of x in equation (1), h = 20√3
Hence the heights of the poles are 20√3 m each and the distances of the point from poles are 20 m and 60 m respectively.
Question 11:
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joing this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see Fig. 9.12). Find the height of the tower and the width of the canal.
एक नहर के एक तट पर एक टीवी टॉवर उर्ध्वार्धर खड़ा है टॉवर के ठीक सामने दूसरे तट के एक अन्य बिंदु से टॉवर के शिखर का उन्नयन कोण 60° है। इसी तट पर इस बिंदु से 20 m दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिंदु से टावर के शिखर का उन्नयन कोण 30° है । टॉवर की ऊँचाई और नहर की चैड़ाई ज्ञात कीजिए।
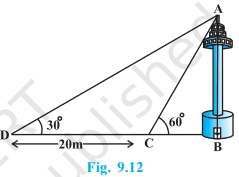
Solution
let AB = h m and BC = x m
In ΔABC,
\(\frac{AB}{BC}\) = tan 60º
\(\frac{h}{x}\) = √3
h = x √3
In ΔABD,
\(\frac{AB}{BD}\) = tan 30º
\(\frac{h}{x + 20}\) = \(\frac{1}{√3}\)
h√3 = x + 20
x √3 \(\times\) √3 = x + 20
3 x – x = 20
2x = 20
x = 10m
and h = 10 √3
Hence height of the tower is 10√3 m and the width of the canal is 10 m.
Question 12:
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
7 m ऊँचे भवन के शिखर से एक केबल टावर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45o है। टॉवर की ऊँचाई ज्ञात कीजिए।
Solution
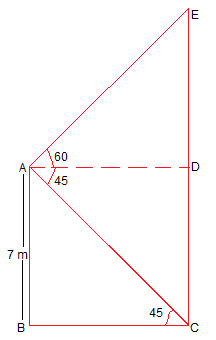
let BC = AD = x m and EC = h m and ED = (h – 7) m
In ΔABC,
\(\frac{AB}{BC}\) = tan 45º
\(\frac{7}{x}\) = 1
x = 7 m
In ΔADE,
\(\frac{ED}{AD}\) = tan 60º
\(\frac{h – 7}{x}\) = √3
h – 7 = √3 x
h – 7 = 7√3
h = 7√3 + 7 = 7[√3 + 1]m
Hence height of the tower is 7[√3 + 1]m.
Question 13:
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
समुद्र-तल से 75 m ऊँची लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण 30° और 45° हैं। यदि लाइट हाउस के एक ही ओर एक जहाज दूसरे जहाज के ठीक पीछे हो तो दो जहाजों के बीच की दूरी ज्ञात कीजिए।
Solution
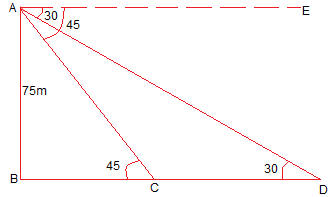
Let BC = x m and CD = y m
In ΔABC,
\(\frac{AB}{BC}\) = tan 45º
\(\frac{75}{x}\) = 1
x = 75
In ΔABD,
\(\frac{AB}{BD}\) = tan 30º
\(\frac{75}{x + y}\) =\(\frac{1}{√3}\)
x + y = 75 √3
75 + y = 75 √3
y = 75 √3 – 75 = 75 [√3 – 1]
Hence the distance between the two ships is 75[√3 – 1]m
Question 14:
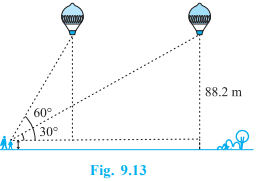
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see Fig. 9.13). Find the distance travelled by the balloon during the interval.
1.2 m लंबी एक लड़की भूमि से 88.2 m की ऊँचाई पर एक क्षैतिज रेखा में हवा में उड़ रहे गुब्बारे को देखती है। किसी भी क्षण लड़की की आँख से गुब्बारे का उन्नयन कोण 60° है। कुछ समय बाद उन्नयन कोण घटकर 30° हो जाता है | इस अन्तराल के दौरान गुब्बारे द्वारा तय की गयी दुरी ज्ञात कीजिए |
Solution
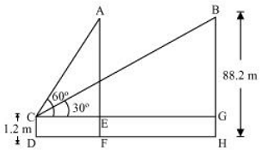
CD = EF = GH = 1.2 m
Let CE = x m and EG = y m
AE = BG = (88.2 – 1.2) = 87 m
In ΔACE,
\(\frac{AE}{CE}\) = tan 60º
\(\frac{87}{x\) = √3
x = \(\frac{87}{√3}\) = \(\frac{87√3}{3}\) = 29 √3
In ΔBCG,
\(\frac{BG}{CG}\) = tan 30º
\(\frac{87}{x + y}\) = \(\frac{1}{√3}\)
x + y = 87√3
29 √3 + y = 87 √3
y = 87 √3 – 29 √3 = 58 √3
Distance travelled by balloon = EG 58√3m
Hence the distance travelled by the balloon during the interval is 58√3 m.
Question 15:
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
एक सीध राजमार्ग एक मीनार के पाद तक जाता है। मीनार के शिखर पर खड़ा एक आदमी एक कार को 30° के अवनमन कोण पर देखता है जो कि मीनार के पाद की ओर एक समान चाल से जाता है। छः सेकंड बाद कार का अवनमन कोण 60° हो गया। इस बिंदु से मीनार के पाद तक पहुँचने में कार द्वारा लिया गया समय ज्ञात कीजिए।
Solution
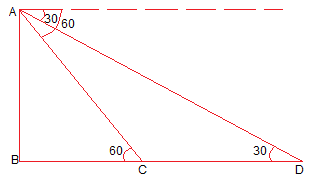
Let BC = distantce travelled = x m
and CD = y m
let AB be h m
In ΔABC,
\(\frac{AB}{BC}\) = tan 60º
\(\frac{h}{x}\) = √3
h = x√3 … (1)
In ΔABD,
\(\frac{AB}{BD}\) = tan 30º
\(\frac{h}{x + y}\) = \(\frac{1}{√3}\)
h√3 = x + y
√3 \(\times\) √3 = x + y
3x = x + y
2x = y
DE = distance = y m
time taken, t = 6 sec
speed = \(\frac{distance}{time}\) = \(\frac{y}{6}\)
uniform speed,
CB, Speed = \(\frac{y}{6}\) m/sec
CB = Distance = x m
time, t = \(\frac{distance}{time}\) = \(\frac{x}{\frac{y}{6}}\)
t = \(\frac{6x}{y}\) = \(\frac{6x}{2x}\) = 3 sec
Hence, the further time taken by the car to reach the foot of the tower is 3 seconds.
NCERT Solutions for Class 10 Maths Chapter 9 Some Application of Trigonometry त्रिकोणमिति के कुछ अनुप्रयोग

