NCERT Solutions of Class 9 Maths Chapter 6 Lines and Angles रेखाएँ और कोण
Important Questions for Class 9 Maths Chapter 6
Thank you for reading this post, don't forget to subscribe!
Table of Contents
Exercise 6.1
Question 1:
In Fig. 6.13, lines AB and CD intersect at O. If ∠ AOC + ∠ BOE = 70° and ∠ BOD = 40°, find ∠ BOE and reflex ∠ COE.
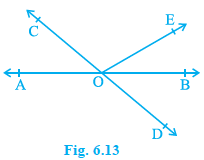
Solution
\(\quad\)∠AOC + ∠COE + ∠BOE = 180° (linear pair)
But ∠ AOC + ∠ BOE = 70° (Given)
\(\Rightarrow\) 70° + ∠COE = 180°
\(\Rightarrow\) ∠COE = 180° – 70° = 110°
and, ∠COE + ∠BOE + ∠BOD = 180° (Linear pair)
\(\Rightarrow\) 110° + ∠BOE + 40° = 180°
\(\Rightarrow\) ∠BOE + 150° = 180°
\(\Rightarrow\) ∠BOE = 180° – 150° = 30°
And, reflex ∠COE = 360° – ∠COE = 360° – 110° = 250°
Question 2:
In Fig. 6.14, lines XY and MN intersect at O. If ∠ POY = 90° and a : b = 2 : 3, find c.
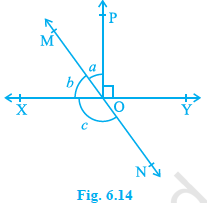
Solution
\(\quad\) ∠ POY = 90° (Given)
\(\quad\) a : b = 2 : 3
Let a = 2x and b = 3x
\(\quad\) ∠XOM + ∠MOP + ∠POY = 180° (linear pair)
\(\Rightarrow\) b + a + 90°= 180°
\(\Rightarrow\) 2x + 3x = 180° – 90°
\(\Rightarrow\) 5x = 90°
\(\Rightarrow\) x = \(\frac{90^o}{5}\) = 18°
Now,
\(\quad\) b + c = 180° \(\Rightarrow\) 3x + c = 180°
\(\Rightarrow\) 3(18°) + c = 180°
\(\Rightarrow\) c = 180° – 54°
\(\Rightarrow\) c = 126°
Question 3:
In Fig. 6.15, ∠ PQR = ∠ PRQ, then prove that ∠ PQS = ∠ PRT.
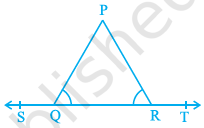
Solution
∠ PQR + ∠ PQS = 180° … (1) (linear pair)
∠ PRQ + ∠ PRT = 180° … (2) (linear pair)
From (1) and (2) ,
∠ PQR + ∠ PQS = ∠ PRQ + ∠ PRT
But, ∠ PQR = ∠ PRQ (given)
\(\Rightarrow\) ∠ PQ5 = ∠ PRT
Question 4:
In Fig. 6.16, if x + y = w + z, then prove that AOB is a line.
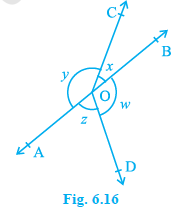
Solution
\(\quad\) x + y + z + w = 360° (central angle)
But x + y = w + z (given)
\(\Rightarrow\) x + y + x + y = 360°
\(\Rightarrow\) 2 (x + y) = 360°
\(\Rightarrow\) x + y = 180°
Linear pair
So, AOB is a line.
Question 5:
In Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays
OP and OR. Prove that ∠ ROS = \(\frac{1}{2}\) (∠ QOS – ∠ POS).
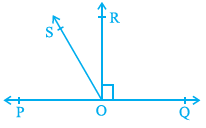
Solution
\(\quad\)OR \(\perp\)PQ
\(\quad\) ∠POR = ∠QOR
\(\Rightarrow\) ∠POS + ∠ROS = ∠QOS – ∠ROS
\(\Rightarrow\) ∠ROS + ∠ROS = ∠QOS – ∠POS
\(\Rightarrow\) 2 ∠ROS = ∠QOS – ∠POS
\(\Rightarrow\) ∠ROS = \(\frac{1}{2}\) (∠ QOS – ∠ POS)
Question 6:
It is given that ∠ XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ ZYP, find ∠ XYQ and reflex ∠ QYP.
Solution
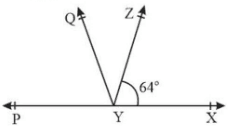
Since, YQ bisects ∠ ZYP \(\Rightarrow\) ∠QYP = ∠ZYQ
\(\quad\)∠XYZ + ∠ZYQ + ∠QYP = 180° (linear pair)
\(\Rightarrow\)64° + ∠QYP + ∠QYP = 180°
\(\Rightarrow\) 2∠QYP = 180°- 64° = 116°
\(\Rightarrow\) ∠QYP = 58°
Also, ∠QYP = ∠ZYQ = 58°
And, ∠XYQ = ∠XYZ + ∠ZYQ = 64° + 58° = 122°
and, reflex ∠QYP = 360° – 58°= 302°
NCERT Solutions of Class 9 Maths Chapter 6 Lines and Angles
Exercise 6.2
Question 1:
In Fig. 6.23, if AB || CD, CD || EF and y : z = 3 : 7, find x.
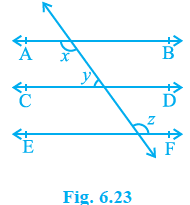
Solution
Question 2:
In Fig. 6.24, if AB || CD, EF ⊥ CD and ∠ GED = 126°, find ∠ AGE, ∠ GEF and ∠ FGE.
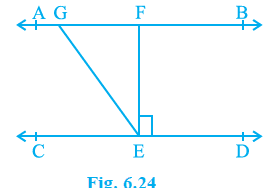
Question 3:
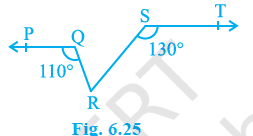
In Fig. 6.25, if PQ || ST, ∠ PQR = 110° and ∠ RST = 130°, find ∠ QRS.
Question 4:
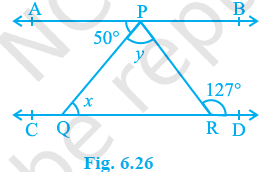
In Fig. 6.26, if AB || CD, ∠ APQ = 50° and ∠ PRD = 127°, find x and y.
Question 5:
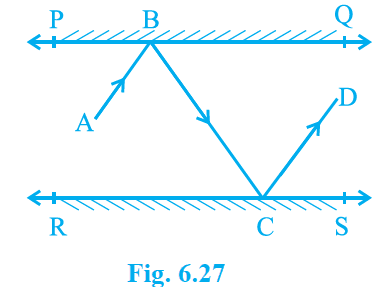
In Fig. 6.27, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.
NCERT Solutions of Class 9 Maths Chapter 6 Lines and Angles

