NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry
Table of Contents
Exercise 8.1
Question 1:
In \(\triangle\) ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine :
(i) sin A, cos A
(ii) sin C, cos C
Solution
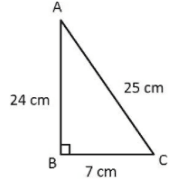
By Pythagoras theorem,
AC2 = AB2 + BC2
AC2 = 242 + 72 = 576 + 49 = 625
AC2 = 252
AC = 25 cm
(i) \(\sin A = \frac{P}{H} = \frac{BC}{AC} = \frac{7}{25} \\[6pt]
\; \cos A = \frac{B}{H} = \frac{AB}{AC} = \frac{24}{25} \)
(ii) \(\sin C = \frac{P}{H} = \frac{AB}{AC} = \frac{24}{25} \\[6pt]
\cos C = \frac{B}{H} = \frac{BC}{AC} = \frac{7}{25}
\)
Question 2:
In Fig. 8.13, find tan P – cot R.
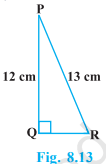
Solution
By Pythagoras theorem,
PR2 = PQ2 + QR2
132 = 122 + QR2
169 = 144 + QR2
169 – 144 = QR2
QR2 = 25
QR2 = 52
QR = 5 cm
Now,
\(\tan P – \cot R\) = \(\frac{P}{B}\) – \(\frac{B}{P}\)
\(\quad\quad\quad = \frac{QR}{PQ}\) – \(\frac{QR}{PQ}\)
\(\quad\quad\quad = \frac{5}{12}\) – \(\frac{5}{12}\) = 0
Question 3:
If sin A = \(\frac{3}{4}\), calculate cos A and tan A.
Solution
sin A = \(\frac{3}{4} = \frac{P}{H}\)
By Pythagoras theorem,
H2 = P2 + B2
42 = 32 + B2
16 = 9 + B2
B2 = 16 – 9 = 7
B= \(\sqrt{7}\)
Now,
\(\cos A = \frac{B}{H} = \frac{\sqrt{7}}{4}\\[6pt]
\tan A = \frac{P}{B} = \frac{3}{\sqrt{7}}\)
Question 4:
Given 15 cot A = 8, find sin A and sec A.
Solution
15 cot A = 8
cot A = \(\frac{8}{15} = \frac{B}{P}
\\[6pt]\)
By Pythagoras theorem,
H2 = P2 + B2
H2 = 152 + 82 = 225 + 64 = 289 = 172
H = 17
Now,
sin A = \(\frac{P}{H}\) = \(\frac{15}{17}\)
sec A = \(\frac{H}{B}\) = \(\frac{17}{8}\)
Question 5:
Given sec \(\theta\) = \(\frac{13}{12}\) , calculate all other trigonometric ratios.
Solution
sec \(\theta\) = \(\frac{13}{12} = \frac{H}{B}\)
By Pythagoras theorem,
H2 = P2 + B2
132 = P2 + 122
169 = P2 + 144
P2 = 169 – 144 = 25 = 52
P = 5
Now,
\(\sin A = \frac{P}{H}= \frac{5}{13}\\[4pt]
\cos A = \frac{B}{H}= \frac{12}{13}\\[4pt]
\tan A = \frac{P}{B}= \frac{5}{12}\\[4pt]
\csc A = \frac{H}{P}= \frac{13}{5}\\[4pt]
\cot A = \frac{B}{P}= \frac{12}{5}\\[4pt]\)
Question 6:
If ∠ A and ∠ B are acute angles such that cos A = cos B, then show that ∠ A = ∠ B.
Solution
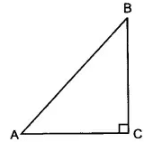
Since ∠A and ∠B are acute angles, then ∠C = 90o
\(\quad\)cos A = cos B (Given)
\(\Rightarrow \frac{AC}{AB} = \frac{BC}{AB}\)
\(\Rightarrow AC = BC\)
\(\therefore\) ∠A = ∠B [Opposite angles to equal sides are equal]
Question 7:
If \(\cot {\theta}\) = \(\frac{7}{8}\), evaluate: (i) \(\frac{(1 + \sin {\theta})(1 – \sin {\theta})}{(1 + \cos {\theta})(1- \cos {\theta})}\), (ii) \(\cot^2 {\theta}\)
Solution
\(\cot {\theta}\) = \(\frac{7}{8} = \frac{B}{P}\)
By Pythagoras theorem,
H2 = P2 + B2 = 82 + 72 = 64 + 49 = 113
H = \(\sqrt{113}\)
(i) \(\frac{(1 + \sin {\theta})(1 – \sin {\theta})}{(1 + \cos {\theta})(1- \cos {\theta})}\\[6pt]
= \frac{(1 + \frac{P}{H})(1 – \frac{P}{H})}{(1 + \frac{B}{H})(1- \frac{B}{H})}\\[6pt]\)
\(= \frac{(1 + \frac{8}{\sqrt{113}})(1 – \frac{8}{\sqrt{113}})}{(1 + \frac{7}{\sqrt{113}})(1- \frac{7}{\sqrt{113}})}\\[6pt]\)
\(= \frac{(1)^2 – \left(\frac{8}{\sqrt{113}}\right)^2}{(1)^2 – \left(\frac{7}{\sqrt{113}}\right)^2}\) [(A + B) (A – B) = A2 – B2]
\(= \frac{1 – \frac{64}{113}}{1 – \frac{49}{113}}\\[6pt]\)
\(= \frac{\frac{113 – 64}{113}}{\frac{113 – 49}{113}}\)
= \(\frac{49}{64}\)
(ii) \(\cot^2 {\theta}\)
= \(\left(\frac{7}{8}\right)^2\)
= \(\frac{49}{64}\)
Question 8:
If 3 cot A = 4, check whether \(\frac{1 – \tan^2 A}{1 + \tan^2 A}\) = \(\cos^2 A\) – \(\sin^2 A\) or not.
Solution
3 cot A = 4
cot A = \(\frac{4}{3} = \frac{B}{P}\)
By Pythagoras theorem,
H2 = P2 + B2 = (3)2 + (4)2 = 9 + 16 = 25 = 52
H = 5
Now, tan A = \(\frac{P}{B} = \frac{3}{4}\)
cos A = \(\frac{B}{H} = \frac{4}{5}\)
sin A = \(\frac{P}{H} = \frac{3}{5}\)
LHS
= \(\frac{1 – \tan^2 A}{1 + \tan^2 A}\)
= \(\frac{1 – \left(\frac{3}{4}\right)^2}{1 + \left(\frac{3}{4}\right)^2}\)
Question 9:
In triangle ABC, right-angled at B, if tan A = \(\frac{1}{\sqrt{3}}\), find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Solution
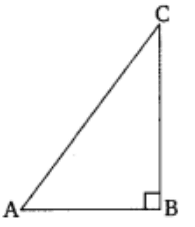
tan A = \(\frac{1}{\sqrt{3}} = \frac{BC}{AC}\)
By Pythagoras theorem,
Question 10:
In \(\triangle\) PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Question 11:
State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = \(\frac{12}{5}\) for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin \(\theta\) = \(\frac{4}{3}\) for some angle \(\theta\).
Solution
i) False.
In ΔABC in which ∠B = 90º, AB = 3, BC = 4 and AC = 5 Value of tan A = 4/3 which is greater than 1.
(ii) True.
Let a ΔABC in which ∠B = 90º,AC be 12k and AB be 5k, where k is a positive real number.
By Pythagoras theorem we get, AC 2 = AB 2 + BC 2 (12k) 2 = (5k) 2 + BC 2 BC 2 + 25k 2 = 144k 2 BC 2 = 119k 2
Such a triangle is possible as it will follow the Pythagoras theorem.
(iii) False.
Abbreviation used for cosecant of angle A is cosec A.
cos A is the abbreviation used for cosine of angle A.
(iv) False.
cot A is not the product of cot and A. It is the cotangent of ∠A.
(v) False. sin θ = Height/Hypotenuse We know that in a right angled triangle, Hypotenuse is the longest side.
∴ sin θ will always less than 1 and it can never be 4/3 for any value of θ.
Exercise 8.2
Question 1:
Evaluate the following :
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan2 45° + cos2 30° – sin2 60°
(iii) \(\frac{\cos {45°}}{\sec {30°} + cosec {30°}}\)
(iv) \(\frac{\sin {30°} + \tan {45° – cosec {60°}}}{\sec {30°} + \cos {60°} + \cot {45°}}\)
(v) \(\frac{5\cos^2 {60°} + 4\sec^2 {30°} – \tan^2 {45°}}{\sin^2 {30°} + \cos^2 {30°}}\)
Solution
(i) sin 60° cos 30° + sin 30° cos 60°
\(\quad\) = \(\frac{\sqrt{3}}{2} \times\) \(\frac{\sqrt{3}}{2}\) + \(\frac{1}{2} \times\) \(\frac{1}{2}\)
\(\quad\) = \(\frac{3}{4} \) + \(\frac{1}{4}\)
\(\quad\) = \(\frac{4}{4}\) = 1
(ii) 2 tan2 45° + cos2 30° – sin2 60°
\(\quad\) = 2 (1)2 + \((\frac{\sqrt{3}}{2})^2\) – \((\frac{\sqrt{3}}{2})^2\)
\(\quad\) = 2
(iii) \(\frac{\cos {45°}}{\sec {30°} + cosec {30°}}\)
\(\quad\) = \(\frac{\frac{1}{\sqrt{2}}}{\frac{2}{\sqrt{3}} + 2}\)
\(\quad\) = \(\frac{\frac{1}{\sqrt{2}}}{\frac{2 + 2\sqrt{3}}{\sqrt{3}}}\)
\(\quad\) = \(\frac{1}{\sqrt{2}}\) \(\times\) \(\frac{\sqrt{3}}{2 + 2\sqrt{3}}\)
(iv) \(\frac{\sin {30°} + \tan {45° – cosec {60°}}}{\sec {30°} + \cos {60°} + \cot {45°}}\)
=\(\frac{\frac{1}{2} + 1 – \frac{2}{\sqrt{3}}}{\frac{2}{\sqrt{3}} – \frac{1}{2} + 1}\)
= \(\frac{\frac{\sqrt{3} + 2\sqrt{3} – 4}{2\sqrt{3}}}{\frac{4 + \sqrt{3} + 2\sqrt{3}}{2\sqrt{3}}}\)
= \(\frac{\sqrt{3} + 2\sqrt{3} – 4}{4 + \sqrt{3} + 2\sqrt{3}}\)
=\(\frac{3\sqrt{3} – 4}{3\sqrt{3} + 4}\) \(\times\) \(\frac{3\sqrt{3} – 4}{3\sqrt{3} – 4}\)
= \(\frac{(3\sqrt{3} – 4)^2}{(3\sqrt{3} + 4)(3\sqrt{3} – 4)}\)
= \(\frac{27 + 16 – 24\sqrt{3}}{27 -16}\)
= \(\frac{43 – 24\sqrt{3}}{11}\)
(v) \(\frac{5\cos^2 {60°} + 4\sec^2 {30°} – \tan^2 {45°}}{\sin^2 {30°} + \cos^2 {30°}}\)
= \(\frac{5()^2 + 4()^2 – (1)^2}{(\frac{1}{2})^2 + (\frac{\sqrt{3}}{2})^2}\)
Question 2:
Choose the correct option and justify your choice :
(i) \(\frac{2 \tan {30^o}}{1 + \tan^2 {30^o}}\) =
\(\quad\) (A) \(\sin {60^o}\) (B) \(\cos {60^0}\) (C) \(\tan {60^0}\) (D) \(\sin {30^0}\)
Question 3:
If tan (A + B) = \(\sqrt{3}\) and tan (A – B) = \(\frac{1}{\sqrt3}\); 0° < A + B \(\le\) 90°; A > B, find A and B.
Solution
tan (A + B) = 3 \(\Rightarrow\)
and tan (A – B) = \(\frac{1}{\sqrt3}\)
Question 4:
State whether the following are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin \(\theta\) increases as \(\theta\) increases.
(iii) The value of cos \(\theta\) increases as \(\theta\) increases.
(iv) sin \(\theta\) = cos \(\theta\) for all values of \(\theta\).
(v) cot A is not defined for A = 0°.
Exercise 8.3
Question 1:
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Question 2:
Write all the other trigonometric ratios of \(\angle\) A in terms of sec A.
Solution
We know that \( \sin^2 A + \cos^2 A = 1\),
\(\Rightarrow\) \( \sin^2 A = 1 – \cos^2 A \) = 1 – \(\frac{1}{sec^2 A} \)
= \(\frac{sec^2 A – 1}{sec^2 A} \\[6pt]
\Rightarrow \sin A = \sqrt{\frac{sec^2 A – 1}{sec^2 A}} = \frac{\sqrt{sec^2 A – 1}}{sec A}\)
and , \( \cos A = \frac{1}{sec A} \)
\( 1 + \tan^2 A = \sec^2 A \)
\(\Rightarrow \tan A = \sqrt{sec^2 A – 1}\)
\(\cot A = \frac{\cos A}{\sin A}
= \frac{\tfrac{1}{\sec A}}{\tfrac{\sqrt{\sec^2 A – 1}}{\sec A}}
= \frac{1}{\sqrt{\sec^2 A – 1}}\)
and,
\(\csc A = \frac{1}{\sin A}
= \frac{\sec A}{\sqrt{\sec^2 A – 1}}\)
Question 3:
Choose the correct option. Justify your choice.
(i). \( 9 \sec^2 A – 9 \tan^2 A = \)
(A) \( 1 \) (B) \( 9 \) (C) \( 8 \) (D) \( 0 \)
(ii). \( (1 + \tan \theta + \sec \theta)(1 + \cot \theta – \csc \theta) = \)
(A) \( 0 \) (B) \( 1 \) (C) \( 2 \) (D) \( -1 \)
(iii). \( (\sec A + \tan A)(1 – \sin A) = \)
(A) \( \sec A \) (B) \( \sin A \) (C) \( \csc A \) (D) \( \cos A \)
(iv). \( \frac{1 + \tan^2 A}{1 + \cot^2 A} = \)
(A) \( \sec^2 A \) (B) \( -1 \) (C) \( \cot^2 A \) (D) \( \tan^2 A \)
Question 4:
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
(i) \(\left( \csc \theta – \cot \theta \right)^2\) = \(\frac{1 – \cos \theta}{1 + \cos \theta}\)
LHS
= \(\left( \csc \theta – \cot \theta \right)^2\)
\(\\\quad\)= \(\left( \frac{1}{\sin \theta} – \frac{\cos \theta}{\sin \theta}\right)^2\)
\(\\\quad\) = \(\left( \frac{1 – \cos \theta}{\sin \theta}\right)^2\)
\(\\\quad\) = \(\frac{\left(1 – \cos \theta\right)^2}{1 – \cos^2 \theta}\)
\(\\\quad\) = \(\frac{(1 – \cos \theta)(1 – \cos \theta)}{(1 + \cos \theta)(1 – \cos \theta)}\)
\(\\\quad\) = \(\frac{1 – \cos \theta}{1 + \cos \theta}\)
\(\\\quad\) = RHS
(ii) \(\frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A}\) = 2\(\sec A\)
LHS
\(\\\quad\) = \(\frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A}\)
\(\\\quad\) = \(\frac{\cos^2 A + (1 + \sin A)^2}{(1 + \sin A) \cos A}\)
\(\\\quad\) = \(\frac{\cos^2 A + 1 + \sin^2 A + 2 \sin A}{(1 + \sin A) \cos A}\)
\(\\\quad\) = \(\frac{\sin^2 A + \cos^2 A + 1 + 2 \sin A}{(1 + \sin A) \cos A}\)
\(\\\quad\) = \(\frac{1 + 1 + 2 \sin A}{(1 + \sin A) \cos A}\)
\(\\\quad\) = \(\frac{2 + 2 \sin A}{(1 + \sin A) \cos A}\)
\(\\\quad\) = \(\frac{2(1 + \sin A)}{(1 + \sin A) \cos A}\)
\(\\\quad\) = \(\frac{2}{\cos A}\)
\(\\\quad\) = 2\(\sec A\)
\(\\\quad\) = RHS

