NCERT Solutions for Class 10 Maths Chapter 14 Probability प्रायिकता
Important Questions for Class 10 Maths Chapter 14 Probability
Thank you for reading this post, don't forget to subscribe!Exercise 14.1
Question 1:
Complete the following statements:
(i) Probability of an event E + Probability of the event ‘not E’ = ________.
(ii) The probability of an event that cannot happen is _____. Such an event is called ________.
(iii) The probability of an event that is certain to happen is _____. Such an event is called ________.
(iv) The sum of the probabilities of all the elementary events of an experiment is ________.
(v) The probability of an event is greater than or equal to ____ and less than or equal to ________.
निम्नलिखित कथनों को पूरा कीजिए :
(i) घटना E की प्रायिकता + घटना ‘E नहीं’ की प्रायिकता = …….. है |
(ii) उस घटना कि प्रायिकता जो घटित नहीं हो सकती ……. है | ऐसी घटना ……. कहलाती है |
(iii) उस घटना कि प्रायिकता जिसका घटित होना निश्चित है ……. है | ऐसी घटना ……. कहलाती है |
(iv) किसी प्रयोग कि सभी प्रारंभिक घटनाओं की प्रायिकताओं का योग …… है |
(v) किसी घटना की प्रायिकता …..से बड़ी या उसके बराबर होती है तथा ……से छोटी या उसके बराबर होती है |
Solution
(i) 1
(ii) 0, impossible event
(iii) 1, sure or certain event
(iv) 1
(v) 0, 1
NCERT Solutions for Class 10 Maths Chapter 14 Probability प्रायिकता
Question 2:
Which of the following experiments have equally likely outcomes? Explain.
(i) A driver attempts to start a car. The car starts or does not start.
(ii) A player attempts to shoot a basketball. She/he shoots or misses the shot.
(iii) A trial is made to answer a true-false question. The answer is right or wrong.
(iv) A baby is born. It is a boy or a girl.
निम्नलिखित प्रयोगों में से किन-किन प्रयोगों के परिणाम समप्रायिक हैं ? स्पष्ट कीजिए |
(i) एक ड्राइवर कार चलाने का प्रयत्न करता है | कार चलना प्रारंभ हो जाती है या कार चलना प्रारंभ नहीं होती है |
(ii) एक खिलाड़ी बास्केटबौल को बास्केट में डालने का प्रयत्न करती है | वह बास्केट में बौल डाल पाती है या नहीं डाल पाती है |
(iii) एक सत्य – असत्य प्रश्न का अनुमान लगाया जाता है | उत्तर सही है या गलत होगा |
(iv) एक बच्चे का जन्म होता है | वह एक लड़का है या एक लड़की है |
Solution
(i) This statement does not have equally likely outcomes as the car may or may not start depending upon various factors like fuel, etc.
(ii) This statement does not have equally likely outcomes as the player may shoot or miss the shot.
(iii) This statement has equally likely outcomes as it is known that the solution is either right or wrong.
(iv) This statement also has equally likely outcomes as it is known that the newly born baby can either be a boy or a girl.
Question 3:
Why is tossing a coin considered to be a fair way of deciding which team should get the ball at the beginning of a football game?
फुटबौल के खेल को प्रांरभ करते समय यह निर्णय लेने के लिए कि कौन सी टीम पहले बौल लेगी, इसके लिए सिक्का उछलना एक न्यायसंगत विधि क्योँ माना जाता है ?
Solution
When we toss a coin, the outcomes head and tail are equally likely. So the result of an individual coin toss is completely unpredicatable.
Question 4:
Which of the following cannot be the probability of an event?
निम्नलिखित में से कौन सी संख्या किसी घटना की प्रायिकता नहीं हो सकती ?
(a) \(\frac{2}{3}\) \(\quad\) (b) – 1.5 \(\quad\) (c) 15 % \(\quad\) (d) 0.7
Solution
(B) -1.5 cannot be the probability of an event.
Since the probability of an event E is a number P(E) such that 0 ≤ P(E) ≤ 1
Question 5:
If P(E) = 0.05, what is the probability of ‘not E’?
यदि P(E) = 0.05 है, तो ‘E नहीं’ कि प्रायिकता क्या है ?
Solution
P(E) + P (not E) = 1
so, P (not E) = 1 – P(E) = 1 – 0.05 = 0.95
Question 6:
A bag contains lemon flavoured candies only. Malini takes out one candy without looking into the bag. What is the probability that she takes out
(i) an orange flavoured candy?
(ii) a lemon flavoured candy?
एक थैले में केवल नींबू कि महक वाली मीठी गोलियाँ हैं | मालिनी बिना थैले में झाँके उसमें से एक गोली निकालती है | इसकी क्या प्रायिकता है कि वह निकाली गई गोली
(i) संतरे कि महक वाली है ?
(ii) नींबू कि महक वाली है ?
Solution
(i) The number of orange-flavoured candies = 0
∴ The probability of taking out orange-flavoured candies = 0/1 = 0
(ii) As there are only lemon-flavoured candies, P(lemon-flavoured candies) = 1
Question 7:
It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?
यह दिया हुआ है कि 3 विधार्थियों के एक समूह में से 2 विधार्थियों के जन्मदिन एक ही दिन न होने कि प्रायिकता 0.9992 है | इसकी क्या प्रायिकता है कि इन 2 विधार्थियों का जन्मदिन एक ही दिन हो ?
Solution
Let E be the event of having the same birthday
Given, P(E) = 0.992
But P(E) + P(not E) = 1
P(not E) = 1 – P(E) = 1 – 0.992 = 0.008
Question 8:
A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is (i) red ? (ii) not red?
एक थैले में 3 लाल और 5 काली गेंदें हैं | इस थैले में से एक गेंद यदृच्छया निकाली जाती है| इसकी प्रायिकता क्या है कि गेंद
(i) लाल हो (ii) लाल नहीं हो ?
Solution
There are 3 + 5 = 8 balls in a bag. Out of these 8 balls, one can be chosen in 8 ways.
so, Total number of elementary events = 8
(i) Since the bag contains 3 red balls, therefore, one red ball can be drawn in 3 ways.
so, Favourable number of elementary events = 3
Hence P (getting a red ball) = \(\frac{3}{8}\)
(ii) Since the bag contains 5 black balls along with 3 red balls, therefore one black (not red) ball can be drawn in 5 ways.
so, Favourable number of elementary events = 5
Hence P (getting a black ball) = \(\frac{5}{8}\)
Question 9:
A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be (i) red ? (ii) white ? (iii) not green?
एक डिब्बे में 5 लाल कंचे, 8 सफेद कंचे और 4 हरे कंचे हैं | इस डिब्बे में से एक कंचा (i) लाल है ? (ii) सफेद है ? (iii) हरा नहीं है ?
Solution
Total number of marbles in the box = 5 + 8 + 4 = 17
so, Total number of elementary events = 17
(i) There are 5 red marbles in the box.
Favourable number of elementary events = 5
so, P (getting a red marble) = \(\frac{5}{17}\) = 0.29
(ii) There are 8 white marbles in the box.
Favourable number of elementary events = 8
So, P (getting a white marble) = \(\frac{8}{17}\) = 0.47
(iii) Total number of green marble = 4
P (green marble) = \(\frac{4}{17}\) = 0.23
∴ P (not green) = 1-P(green ball) = 1 – \(\frac{4}{17}\) = \(\frac{13}{17}\) = 0.77
Question 10:
A piggy bank contains hundred 50p coins, fifty 1 coins, twenty 2 coins and ten 5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, what is the probability that the coin (i) will be a 50 p coin ? (ii) will not be a 5 coin?
एक पिग्गी बैंक (piggy bank) में, 50 पैसे के सौ सिक्के है, 1 रू के पचास सिक्के हैं, 2 रू के बीस सिक्के और 5 के 10 सिक्के हैं | यदि पिग्गी बैंक को हिलाकर उल्टा करने अपर कोई एक सिक्का गिराने के परिणाम समप्रायिक हैं, तो इसकी क्या प्रायिकता है कि वह गिरा हुआ सिक्का
(i) 50 पैसे का होगा ? (ii) 5 रू का नहीं होगा ?
Solution
Total number of coins in a piggy bank = 100 + 50 + 20 + 10 = 180
So, Total number of elementary events = 180
(i) Total number of 50 p coin = 100
P (50 p coin) = 100/180 = 5/9 = 0.55
(ii)Total number of ₹5 coin = 10
P (₹5 coin) = 10/180 = 1/18 = 0.055
∴ P (not ₹5 coin) = 1-P (₹5 coin) = 1-0.055 = 0.945
Question 11:
Gopi buys a fish from a shop for his aquarium. The shopkeeper takes out one fish at random from a tank containing 5 male fish and 8 female fish (see Fig. 14.4). What is the probability that the fish taken out is a male fish?
गोपी अपने जल – जीव कुंड (aquarium) के लिए एक दुकान से मछली खरीदती है | दुकानदार एक टंकी, जिसमें 5 नर मछली और 8 मादा मछली है, में से एक मछली यादृच्छया उसे देने के लिए निकालती है (देखिए आकृति 15.4) | इसकी प्रायिकता है कि निकाली गई मछली नर मछली है ?
Solution
Total number of fish in the tank = 5 + 8 = 13
∴ Total number of elementary events = 13
There are 5 male fishes in the tank.
∴ Favourable number of elementary events = 5
Hence, P (taking out a male fish) = 5/13 = 0.38
Question 12:
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see Fig. 14.5 ), and these are equally likely outcomes. What is the probability that it will point at
(i) 8 ?
(ii) an odd number?
(iii) a number greater than 2?
(iv) a number less than 9?
संयोग (chance) के एक खेल में, एक तीर को घुमाया जाता है, जो विश्राम में आने के बाद संख्याओं 1,2,3,4,5,6,7, और 8 में से किसी एक संख्या को इंगित करता है (देखिए आकृति 14.5) | यदि ये सभी परिणाम समप्रायिक हों तो इसकी क्या प्रायिकता है कि यह तीर इंगित
(i) 8 को करेगा ?
(ii) एक विषम संख्या को करेगा ?
(iii) 2 से बड़ी संख्या को करेगा ?
(iv) 9 से छोटी संख्या को करेगा ?
Solution
Out of 8 numbers, an arrow can point any of the numbers in 8 ways.
∴ Total number of favourable outcomes = 8
(i) Favourable number of outcomes = 1
Hence, P (arrow points at 8) = \(\frac{1}{8}\) = 0.125
(ii) Favourable number of outcomes = 4
Hence, P (arrow points at an odd number) = \(\frac{4}{8}\) = ½ = 0.5
(iii) Favourable number of outcomes = 6
Hence, P (arrow points at a number > 2) = \(\frac{6}{8}\) = \(\frac{3}{4}\) = 0.75
(iv) Favourable number of outcomes = 8
Hence, P (arrow points at a number < 9) = \(\frac{8}{8}\) =1
Question 13:
A die is thrown once. Find the probability of getting
(i) a prime number; (ii) a number lying between 2 and 6; (iii) an odd number.
एक पासे को एक बार फेंका जाता है | निम्नलिखित को प्राप्त करने कि प्रायिकता ज्ञात कीजिए :
(i) एक अभाज्य संख्या (ii) 2 और 6 के बीच स्थित कोई संख्या (iii) एक विषम संख्या
Solution
Total number of favourable outcomes of throwing a dice = 6
(i) On a dice, the prime numbers are 2, 3 and 5.
Therefore, favourable outcomes = 3
Hence P (getting a prime number) = 3/6 = ½ = 0.5
(ii) On a dice, the number lying between 2 and 6 are 3, 4, 5.
Therefore, favourable outcomes = 3
Hence P (getting a number lying between 2 and 6) = 3/6 = ½ = 0.5
(iii) On a dice, the odd numbers are 1, 3 and 5.
Therefore, favourable outcomes = 3
Hence P (getting an odd number) = 3/6 = ½ = 0.5
Question 14:
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting
(i) a king of red colour (ii) a face card (iii) a red face card (iv) the jack of hearts (v) a spade (vi) the queen of diamonds
52 पत्तों कि अच्छी प्रकार से फेटी गई एक गड्डी में से एक पत्ता निकला जाता है | निम्नलिखित को प्राप्त करने कि प्रायिकता ज्ञात कीजिए :
(i) लाल रंग का बादशाह (ii) एक फेस कार्ड अर्थात् तस्वीर वाला पत्ता (iii) लाल रंग का तस्वीर वाला पत्ता (iv) पान का गुलाम (v) हुकुम का पत्ता (vi) एक ईंट कि बेगम
Solution
Total number of favourable outcomes = 52
(i) There are two suits of red cards, i.e., diamond and heart. Each suit contains one king.
∴ Favourable outcomes = 1
Hence, P (a king of red colour) = 2/52 = 1/26 = 0.038
(ii) There are 12 face cards in a pack.
So, Favourable outcomes = 12
Hence, P (a face card) = 12/52 = 3/13 = 0.23
(iii) There are two suits of red cards, i.e., diamond and heart. Each suit contains 3 face cards.
So, Favourable outcomes = 6
Hence, P (a red face card) = 6/52 = 3/26 = 0.11
(iv) There are only one jack of heart.
So, Favourable outcome = 1
Hence, P (the jack of hearts) = 1/52 = 0.019
(v) There are 13 cards of spade.
So, Favourable outcomes = 13
Hence, P (a spade) = 13/52 = ¼ = 0.25
(vi) There is only one queen of diamonds.
So, Favourable outcome = 1
Hence, P (the queen of diamonds) = 1/52 = 0.019
Question 15:
Five cards—the ten, jack, queen, king and ace of diamonds, are well-shuffled with their face downwards. One card is then picked up at random.
(i) What is the probability that the card is the queen?
(ii) If the queen is drawn and put aside, what is the probability that the second card picked up is (a) an ace? (b) a queen?
ताश के पाँच पत्तों – ईंट का दहला, गुलाम, बेगम, बादशाह और इक्का – को पलट करके अच्छी प्रकार फेटा जाता है | फिर इनमें से यादृच्छया एक पत्ता निकाला जाता है |
(i) इसकी क्या प्रायिकता है कि यह पत्ता एक बेगम है |
(ii) यदि बेगम निकल आती है, तो उसे अलग रख दिया जाता है और एक अन्य निकाला जाता है | इसकी क्या प्रायिकता है कि दूसरा निकाला गया पत्ता (a) एक इक्का है ? (b) एक बेगम है ?
Solution
Total number of favourable outcomes = 5
(i) There is only one queen.
Favourable outcome = 1
Hence, P (the queen) = ⅕ = 0.2
(ii) In this situation, total number of favourable outcomes = 4
(a) Favourable outcome = 1
Hence, P (an ace) = ¼ = 0.25
(b) There is no card as queen.
So, Favourable outcome = 0
Hence, P (the queen) = 0/4 = 0
Question 16:
12 defective pens are accidentally mixed with 132 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is a good one.
किसी कारण 12 खराब पेन 132 अच्छे पेनों में मिल गए हैं | केवल देखकर यह नहीं बताया जा सकता है कि कोई पेन खराब है या अच्छा है | इस मिश्रण में से, एक पेन यादृच्छया निकाला जाता है | निकले गए पेन कि अच्छा होने कि प्रायिकता ज्ञात कीजिए |
Solution
Total number of favourable outcomes = 132 + 12 = 144
Number of favourable outcomes = 132
Hence, P (getting a good pen) = 132/144 = 11/12 = 0.916
Question 17:
(i) A lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
(ii) Suppose the bulb drawn in (i) is not defective and is not replaced. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective ?
(i) 20 बल्बों के एक समूह में 4 बल्ब खराब हैं | इस समूह में से एक बल्ब यादृच्छया निकाला जाता है| इसकी क्या प्रायिकता है कि यह बल्ब खराब होगा ?
Solution
(i) Total number of favourable outcomes = 20
Number of favourable outcomes = 4
Hence P (getting a defective bulb) = 4/20 = ⅕ = 0.2
(ii) Now total number of favourable outcomes = 20 – 1 = 19
Number of favouroable outcomes = 19 – 4 = 15
Hence P (getting a non-defective bulb) = 15/19 = 0.789
Question 18:
A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears (i) a two-digit number (ii) a perfect square number (iii) a number divisible by 5.
एक पेटी में 90 डिस्क (discs) हैं, जिन पर 1 से 90 तक संख्याएँ अंकित हैं | यदि इस पेटी में से एक डिस्क यादृच्छया निकाली जाती है तो इसकी प्रायिकता ज्ञात कीजिए कि इस डिस्क पर अंकित होगी :
(i) दो अंकों कि एक संख्या (ii) एक पूर्ण वर्ग संख्या (iii) 5 से विभाज्य एक संख्या |
Solution
Total number of favourable outcomes = 90
(i) Number of two-digit numbers from 1 to 90 are 90 – 9 = 81
So, Favourable outcomes = 81
Hence, P (getting a disc bearing a two-digit number) = 81/90 = 9/10 = 0.9
(ii) From 1 to 90, the perfect squares are 1, 4, 9, 16, 25, 36, 49, 64 and 81.
so, Favourable outcomes = 9
Hence P (getting a perfect square) = 9/90 = 1/10 = 0.1
(iii) The numbers divisible by 5 from 1 to 90 are 18.
So, Favourable outcomes = 18
Hence P (getting a number divisible by 5) = 18/90 = ⅕ = 0.2
Question 19:
A child has a die whose six faces show the letters as given below:
एक बच्चे के पास ऐसा पासा है जिसके फलकों पर निम्नलिखित अक्षर अंकित है :

The die is thrown once. What is the probability of getting (i) A? (ii) D?
इस पासे को एक बार फेंका जाता है | इसकी क्या प्रायिकता है कि (i) A प्राप्त हो ? (ii) D प्राप्त हो ?
Solution
Total number of favourable outcomes = 6
(i) Number of favourable outcomes = 2
Hence P (getting a letter A) = 2/6 = ⅓ = 0.33
(ii) Number of favourable outcomes = 1
Hence P (getting a letter D) = ⅙ = 0.166
Question 20:
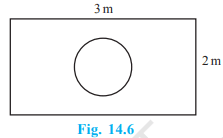
Suppose you drop a die at random on the rectangular region shown in Fig. 14.6. What is the probability that it will land inside the circle with diameter 1m?
मान लीजिये आप एक पासे को आकृति 15.6 में दर्शाए आयताकार क्षेत्र में यादृच्छया रूप से गिराते हैं | इसकी क्या प्रायिकता है कि वह पासा 1 मी व्यास वाले वृत्त के अन्दर गिरेगा ?
Solution
First, calculate the area of the rectangle and the area of the circle. Here, the area of the rectangle is the possible outcome and the area of the circle will be the favourable outcome.
So, the area of the rectangle = (3×2) m 2 = 6 m 2
and,
The area of the circle = πr 2 = π(½) 2 m 2 = π/4 m 2 = 0.78
∴ The probability that die will land inside the circle = [(π/4)/6] = π/24 or, 0.78/6 = 0.13
Queston 21:
A lot consists of 144 ball pens of which 20 are defective and the others are good. Nuri will buy a pen if it is good, but will not buy if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that
(i) She will buy it ?
(ii) She will not buy it ?
144 बाल पेनों के एक समूह में 20 बाल पेन खराब हैं और शेष अच्छे हैं | आप वाही पेन खरीदना चाहेंगे जो अच्छा हो, परन्तु खराब पेन आप खरीदना नहीं चाहेंगे | दुकानदार इन पेनों में से, यादृच्छया एक पेन निकालकर आपको देता है | इसकी क्या प्रायिकता है कि
(i) आप वह पेन खरीदेंगे ?
(ii) आप वह पेन नहीं खरीदेंगे ?
Solution
Total number of favourable outcomes = 144
(i) Number of non-defective pens = 144 – 20 = 124
So, Number of favourable outcomes = 124
Hence P (she will buy) = P (a non-defective pen) = 124/144 = 31/36 = 0.86
(ii) Number of favourable outcomes = 20
Hence P (she will not buy) = P (a defective pen) = 20/144 = 5/36 = 0.138
Question 22:
Refer to Example 13. (i) Complete the following table:
उदाहरण 13 को देखिए | (i) निम्नलिखित सारणी को पूरा कीजिए :

(ii) A student argues that ‘there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Therefore, each of them has a probability \(\frac{1}{12}\). Do you agree with this argument? Justify your answer
(ii) एक विधार्थी यह तर्क देता है कि ‘यहाँ कुल 11 परिणाम 2,3,4,5,6,7,8,9,10,11 और 12 है | अतः प्रत्येक कि प्रायिकता 1/11 है|’ क्या आप इस तर्क से सहमत है ? सकारण उत्तर दीजिए |
Solution
Total favourable outcomes of throwing two dice are:
(1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6)
(2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)
(3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6)
(4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)
(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)
(6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6)
Total number of favourable outcomes = 36
(i) It is given that to get the sum as 2, the probability is 1/36 as the only possible outcomes = (1,1)
For getting the sum as 3, the possible events (or outcomes) = E (sum 3) = (1,2) and (2,1)
So, P(sum 3) = 2/36
Similarly,
E (sum 4) = (1,3), (3,1), and (2,2)
So, P (sum 4) = 3/36
E (sum 5) = (1,4), (4,1), (2,3), and (3,2)
So, P (sum 5) = 4/36
E (sum 6) = (1,5), (5,1), (2,4), (4,2), and (3,3)
So, P (sum 6) = 5/36
E (sum 7) = (1,6), (6,1), (5,2), (2,5), (4,3), and (3,4)
So, P (sum 7) = 6/36
E (sum 8) = (2,6), (6,2), (3,5), (5,3), and (4,4)
So, P (sum 8) = 5/36
E (sum 9) = (3,6), (6,3), (4,5), and (5,4)
So, P (sum 9) = 4/36
E (sum 10) = (4,6), (6,4), and (5,5)
So, P (sum 10) = 3/36
E (sum 11) = (5,6), and (6,5)
So, P (sum 11) = 2/36
E (sum 12) = (6,6)
So, P (sum 12) = 1/36
So, the table will be as:

(ii) I do not agree with the argument given here. Justification has already been given in part (i).
Question 23:
A game consists of tossing a one rupee coin 3 times and noting its outcome each time. Hanif wins if all the tosses give the same result i.e., three heads or three tails, and loses otherwise. Calculate the probability that Hanif will lose the game.
एक खेल में एक रूपए के सिक्के को तीन बार उछाला जाता है और प्रत्येक बार का परिणाम लिख लिया जाता है | तीनों परिणाम समान होने पर, अर्थात् तीन चित या तीन पट प्राप्त होने पर, हनीफ खेल में जीत जाएगा, अन्यथा वह हार जाएगा | हनीफ के खेल में हार जाने कि प्रायिकता परिकलित कीजिए |
Solution
The outcomes associated with the experiment in which a coin is tossed thrice:
HHH, HHT, HTH, THH, TTH, HTT, THT, TTT
Therefore, Total number of favourable outcomes = 8
Number of favourable outcomes = 6
Hence required probability = 6/8 = ¾ = 0.75
Question 24:
A die is thrown twice. What is the probability that
(i) 5 will not come up either time? (ii) 5 will come up at least once?
एक पासे को दो बार फेंका जाता है | इसकी क्या प्रायिकता है कि
(i) 5 किसी भी बार में नहीं आएगा ? (ii) 5 कम से कम एक बार आएगा ?
Solution
(i) The outcomes associated with the experiment in which a dice is thrown is twice:
(1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6)
(2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)
(3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6)
(4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)
(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)
(6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6)
Therefore, Total number of favourable outcomes = 36
Let
A = 5 comes in first throw,
B = 5 comes in second throw
P(A) = 6/36, P(B) = 6/36 and P(not B) = 5/6
So, P(not A) = 1-(6/36) = 5/6
∴ The required probability = (5/6)×(5/6) = 25/36
(ii)Number of events when 5 comes at least once = 11
∴ The required probability = 11/36
Question 25:
Which of the following arguments are correct and which are not correct? Give reasons for your answer.
(i) If two coins are tossed simultaneously there are three possible outcomes—two heads, two tails or one of each. Therefore, for each of these outcomes, the probability is \(\frac{1}{3}\).
(ii) If a die is thrown, there are two possible outcomes—an odd number or an even number. Therefore, the probability of getting an odd number is \(\frac{1}{2}\).
निम्नलिखित में से कौन से तर्क सत्य है और कौन से तर्क असत्य है ? सकारण उत्तर दीजिए |
(i) यदि दो सिक्कों को एक साथ उछाला जाता है, तो इसके तीन संभावित परिणाम – दो चित, दो पट या प्रत्येक एक बार हैं | अतः इनमें से प्रत्येक परिणाम कि प्रायिकता 1/3 है |
(ii) यदि एक पासे को फेंका जाता है, तो इसके दो संभावित परिणाम- एक विषम संख्या या एक सम संख्या है | अतः एक विषम संख्या ज्ञात करने की प्रायिकता 1/2 है |
Solution
(i) All the possible events are (H,H); (H,T); (T,H) and (T,T)
So, P (getting two heads) = ¼
and, P (getting one of each) = 2/4 = ½
∴ This statement is incorrect.
(ii) Since the two outcomes are equally likely, this statement is correct.

